Consider the cantilever beam problem shown previously in Exercise 8.2 with no axial force (N =0). Assume a plane stress anisotropic model given by Hooke’s law (11.5.1) and governed by the Airy stress function equation (11.5.6). Show that the stress function:

Next show that these stresses satisfy the problem boundary conditions in the usual sense with
exact pointwise specification on y =± c, and only resultant force conditions on the end's x = 0
and x = L. What happens to this solution if we let the material become orthotropic?

Data from exercise 8.2

Show that the Airy function:

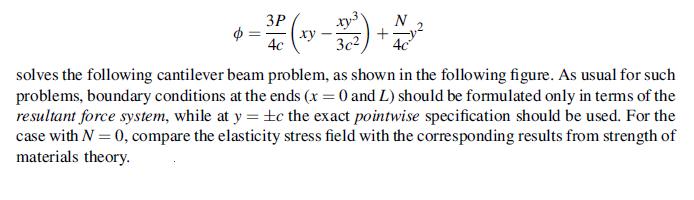
Equation 11.5.1

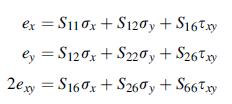
Equation 11.5.6

3P [cxy- 4c3 xy S16 -+ 3 6511 - (26x - y)] satisfies the governing equation and gives the following stress field oy = 0 ty--3 (1-2) = 3P 4c 3P 0x = -2-3x - 2018 (G-2). ox xy+ 3P S16 2c3 S113