For the isotropic self consistent crack distribution case in Example 15 12, show that for the case v 0 5, relation (15 3 4) 3 reduces to Verify the total loss of moduli at 9 16 Using these results, develop plots of the effective moduli ratios v v,E E, versus the crack density Compare these results ...

Isotropic Self Consistent Crack Distribution Case with v05 45VV2V 4505V2v 16110v 3vvv 161V515VV 8 by ...

For the isotropic self-consistent crack distribution case in Example 15.12, show that for the case v =

Question:

For the isotropic self-consistent crack distribution case in Example 15.12, show that for the case v = 0.5, relation (15.3.4)₃ reduces to:

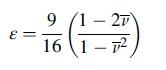
8 = 9 16 - 27 12

Verify the total loss of moduli at ε = 9/
16. Using these results, develop plots of the effective moduli ratios v̅/v,E̅/
E,µ̄/µ versus the crack density. Compare these results with the corresponding values from the dilute case given in Example 15.10.

Data from example 15.10

Data from example 15.12

Using the self-consistent method, effective moduli for the random distribution case can be developed. The results for this case are given by:

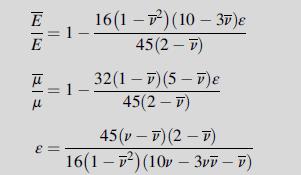
E BI 8 = 1 1 16 (1) (10-3v)e 45(2->) 32(1-7)(5-7) 45(2-7) 45 (v-V) (2-V) 16(1-) (10v 3vv V)

It is interesting to note that as ε→9/16, all effective moduli decrease to zero. This can be interpreted as a critical crack density where the material will lose its coherence. Although it would be expected that such a critical crack density would exist, the accuracy of this particular value is subject to the assumptions of the modeling and is unlikely to match universally with all materials.

Equation 15.3.4

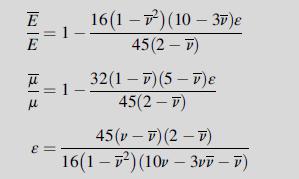
E E u h E 1 16(1-) (103)e 45(2-7) 32(1-7)(5-7)e 45(2-7) 45 (v - V) (2-v) 16(1-)(10v-3v-V)