From strain energy arguments in Section 6.1, it was found that ij /e kl =

Question:

From strain energy arguments in Section 6.1, it was found that ∂σ_ij/∂e_kl = ∂σ_kl/σe_ij. Show that these results imply that C_ij = C_ji, therefore justifying that only 21 independent elastic moduli are needed to characterize the most general anisotropic material.

Data from section 6.1

As mentioned, the work done by surface and body forces on an elastic solid is stored inside the body in the form of strain energy. For an idealized elastic body, this stored energy is completely recoverable when the solid is returned to its original unstrained configuration. In order to quantify this behavior, we now wish to determine the strain energy in terms of the resulting stress and strain fields within the elastic solid. Consider first the simple uniform uniaxial deformation case with no body forces, as shown in Fig. 6.1. The cubical element of dimensions dx, dy, dz is under the action of a uniform normal stress s in the x direction as shown.
During this deformation process, we assume that the stress increases slowly from zero to sx, such that inertia effects can be neglected. The strain energy stored is equal to the net work done on the element, and this is given by the following equation:

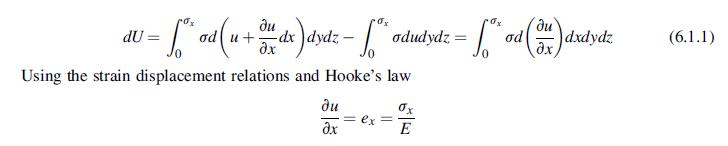
rox * od (u + 3 dx) dydz - [* odudydz = "0 od 0 dx Using the strain displacement relations and Hooke's law