Use the general solution of Exercise 12.12 to solve the thermal stress problem of a hollow thick-walled spherical shell (a ≤ R≤b) with stress-free boundary conditions. Assuming that the problem is steady state with temperature conditions T(a) = T_i, T (b) = 0, show that the solution becomes:

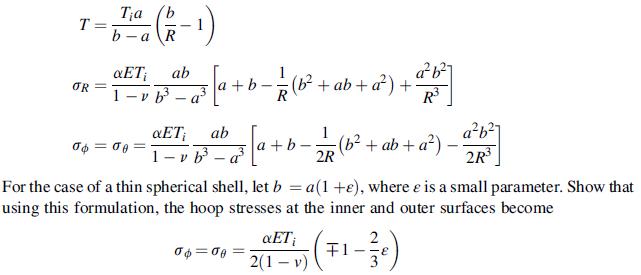
and if we neglect the ε term, these values match those of the cylindrical shell given by relations (12.7.14).

Data from exercise 12.12

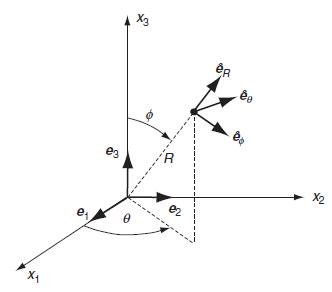
Consider the thermoelastic problem in spherical coordinates (R, ∅, θ); see Fig. 1.6. For the case of spherical symmetry where all field quantities depend only on the radial coordinate R, develop the general solution:

Fig 1.6

Equation 12.7.14

Transcribed Image Text:

T = OR= Ta b-a = (1/2 - ) aETi ab 1-vb-a V = [a+b=_ / / ( b . + - ET; 1-vb ab + ab +a) + 1 [a+b - 2/12 (b + ab + a). 2R ETi 2(1-v) ab7 R For the case of a thin spherical shell, let b = a (1 +e), where e is a small parameter. Show that using this formulation, the hoop stresses at the inner and outer surfaces become 2 *+-%-2 (1-) 0g= ab7 2R