Using the basic field equations for spherical coordinates given in Appendix A, formulate the elasticity problem for
Question:
Using the basic field equations for spherical coordinates given in Appendix A, formulate the elasticity problem for the spherically symmetric case, where uR = u(R), u∅ = uθ = 0. In particular, show that the governing equilibrium equation with zero body forces becomes:

Data from appendix a
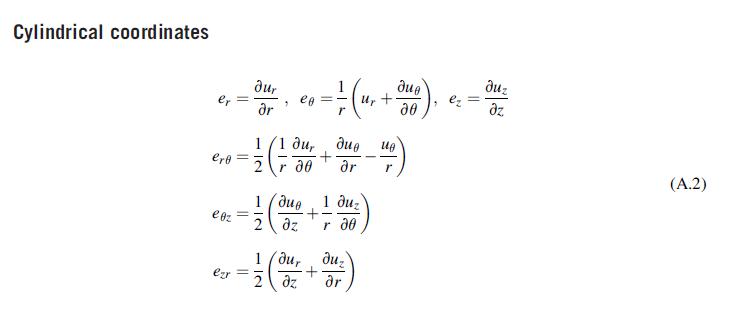
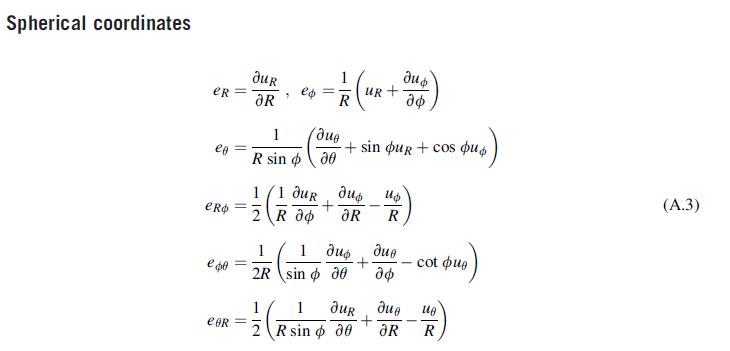
Transcribed Image Text:
2 du 2 du + dR R dR R2 Next solve this equation and show that the general solution can be expressed as C u=CR+ OR = K - R2' 0=08=K+ where C, C2, K, and K are arbitrary constants. 2K2 R3, u=0 K2 R
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 66% (3 reviews)
For the spherically symmetric case U uRu U 0 and relation A12 reduces to du 2 du 2 211 R dR2 ...View the full answer

Answered By

Pharashram rai
i am highly creative, resourceful and dedicated freelancer an excellent record of successful classroom presentations and writing . I have more than 4 years experience in tutoring students especially by using my note making strategies and engineering field . Especially adept at teaching methods of maths and writing , and flexible teaching style with the willingness to work beyond the call of duty. Committed to ongoing professional development and spreading the knowledge within myself to the blooming ones to make them fly with .
4.80+
65+ Reviews
270+ Question Solved
Related Book For 

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.
Question Posted:
Students also viewed these Engineering questions
-
Using the results of Exercise 13.22, solve the problem of a thick-walled spherical shell with inner radius R 1 loaded with uniform pressure p 1 , and with outer radius R 2 loaded with uniform...
-
Using the general solution forms of Exercise 13.22, solve the problem of a rigid spherical inclusion of radius a perfectly bonded to the interior of an infinite body subjected to uniform stress at...
-
Using the results of Exercise 13.22, solve the problem of a stress-free spherical cavity in an infinite elastic medium under uniform far-field stress x = y = z = S. Explicitly show that the...
-
To add new components or tools into the NetBeans IDE, one can use . a. The JFrame tool b. Plugins c. The PHP tool d. JavaFX
-
A vessel at rest at the origin of an xy coordinate system explodes into three pieces. Just after the explosion, one piece, of mass m, moves with velocity (-30 m/s)i and a second piece, also of mass...
-
In the table below, the left column names several classes of transactions. The right column names several general ledger accounts. Required: Identify the general ledger accounts that are affected by...
-
12. What steps must employers take to ensure that they are complying with the Immigration Reform and Control Act?
-
The ABC Partnership is to be liquidated and you have been hired to prepare a Schedule of Cash Payments for the partnership. Partners Andie, Becka, and Candice share income and losses in the ratio of...
-
please answer all the questions thankyou 15. The following transactions were entered into by Dr. Jo Valdez for the month of June: 04 07 08 10 Jo Valdez opened Jo's Health Spa" by investing P1,500,000...
-
Consider the three-dimensional stress concentration problem given in Example 13.5. Recall that the maximum stresses occur on the boundary of the spherical cavity (r = a). With respect to the problem...
-
Using the results of Exercise 13.20, continue the superposition process by combining three force doublets in each of the coordinate directions. This results in a center of dilatation at the origin as...
-
Consider the project with the listed activities, and precedence relationships. Probabilistic durations are given (represented by Beta-distribution). Times are given in weeks. (a) Compute the variance...
-
Analysis of the Volkswagen Scandal Possible Solutions for Recovery The Volkswagen scandal is a notorious example of how corporations can shape the ethical and political issues of the environment. The...
-
Shelby isn't sure if her forklift can safely handle the pallet she is being asked to move. What can she check to be sure
-
If schedule acceleration increases costs, how could schedule elongation reduce costs? If schedule acceleration increases costs, how could schedule elongation reduce costs? For the same total...
-
Laser Care Hospital is looking to raise tax-exempt municipal funds in the bond market. As an issuer of the bond, which of the following is not a part of the bond process that Laser Care Hospital will...
-
Find the critical value t a/2 corresponding to a 95% confidence level. (13.046, 22.15) X= 17.598 Sx= 16.01712719 n=50
-
Use the binomial theorem to compute the following. (x + 2)3
-
Players A, B, and C toss a fair coin in order. The first to throw a head wins. What are their respective chances of winning?
-
Write a script le to play a simple number guessing game as follows. The script should generate a random integer in the range 1, 2, 3, . . . , 14, 15. It should provide for the player to make repeated...
-
Interpolation is useful when one or more data points are missing. This situation often occurs with environmental measurements, such as temperature, because of the difficulty of making measurements...
-
The following table gives temperature data in *C as a function of time of day and day of the week at a specific location. Data are missing for the entries marked with a question mark (?). Use linear...
-
why would an auditor want to complete dual-purpose tests? what procedure can be put into place to help prevent fraud? List 4 procedures.
-
Based on the following information, calculate sustainable growth rate for Groot, Inc.: Profit margin= 7.1% Total asset turnover = 1.90 Total debt ratio = .45 Payout ratio = 20% What is the ROA here?
-
Consider the following: a call option on a stock has strike price $100, premium of $5 and the current price of the underlying stock is $100. If you buy the call option today, what is your holding...

Study smarter with the SolutionInn App


