Using the results of Exercise 13.14, verify that the displacement and stress fields for the Boussinesq problem of Example 13.4 are given by (13.4.20) and (13.4.21). Note the interesting behavior of the radial displacement, that u_r > 0 only for points where z/R > (1– 2v)R/(R + z). Show that points satisfying this inequality lie inside a cone ∅ ≤ ∅_o, with ∅_o determined by the relation cos²∅_o + cos∅_o –(1–2v) = 0.

Data from exercise 13.4

For the axisymmetric case, the Papkovich functions reduced to the Boussinesq potentials B and A_z defined by relations (13.4.11). Show that the general forms for the displacements and stresses in cylindrical coordinates are given by:

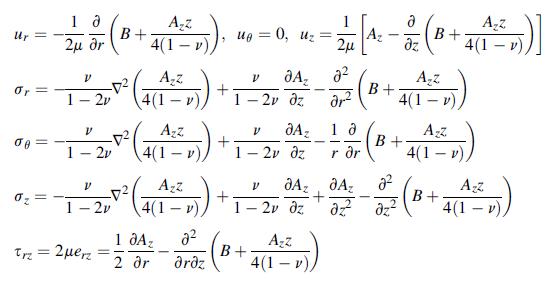
Equation 13.4.11

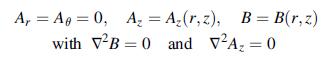
Data from example 13.4

Equation  13.4.20

Equation 13.4.21

Transcribed Image Text:

Mr = 2 &r (8+4 (15)). Ha = 0, Mc= Az B+ r 4(1-v), Or= 0 V Azz V Az 1 06--1-27 (4(1-) +1-2, - (+1) B+ 2v z r r 4(1-v), Trz = V Az V 2 Az 1-200 (4(1-1) + 1 - 20 / (B+ 4(1= n) - 2v v). dz ar 4(1-v) V Azz -D 2 ( 4 (1-1) 1 2v 2uerz 1 Az 2 r 2 rz Az [^- & (8 + 4 (1 - 1)] Az 2 + V JAz Az 2 + 12v dz z z B+ Azz 4(1-v) - B+ 4(1-v)