For a series R–L circuit, it can be shown that the rms (I.E., effective value) of the asymmetrical fault current is given by the following equation

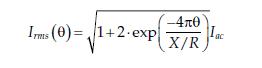
where θ = f × t is time in cycles X = L/ω = 2π × f × L is the reactance of the inductance Iac is the rms of the ac fault current (also called symmetrical fault current)

A short-circuit occurs in a series R–L circuit with V = 277 V, L = 2 mH, R =0.4. Determine

(a) The rms symmetrical fault current

(b) The rms asymmetrical fault current at the instant the switch closes, assuming maximum DC offset

(c) The rms asymmetrical fault current five cycles after the switch closes, assuming maximum DC offset

(d) The DC offset as a function of time if the switch closes when the instantaneous source voltage is 300 V

Irms (0)=1+2-exp -4 X/R)