After several years of research, the company has developed a new grade of CPVC that contains 70.0 wt% chlorine. The high softening temperature and nonflammability of the new material make it suitable for computer cabinets and other potentially profitable products. Plant engineering has determined that the plant can make both the old and the new grades of CPVC, converting the same total amount of PVC per year. The problem is to determine whether or not the production of the 70% Cl grade can be justified economically, and if it can, the fraction of the operating year that should be dedicated to producing each grade.

PVC currently costs $0.70/kg and chlorine costs $0.15/kg. The 67% Cl CPVC sells for $2.50/kg, and 70% Cl CPVC can be sold for $2.90/kg. The manufacturing costs of the two products (which include costs for equipment maintenance and replacement, personnel, utilities, and marketing but do not include the costs of PVC and chlorine) are given by the following functions:

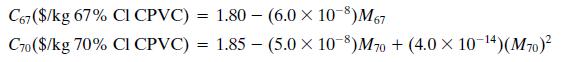
where M₆₇ (kg) and M₇₀(kg) are the masses of each product produced. The second term of each function accounts for the fact that some manufacturing costs (like salaries) are relatively independent of how much product is produced, and so the cost per kilogram of product (C) decreases as the amount of product produced (M) increases. The third term of the second function is a penalty for producing too much of the new product, reflecting costs of additional advertising, sales staff retraining, and additional technical support. (These added costs are expected to disappear after about three years.)

(a) PVC contains 38.4 wt% carbon and 56.8 wt% chlorine; 67% Cl CPVC contains 29.4 wt% carbon and 67.6 wt% chlorine; and 70.0 wt% ClCPVCcontains 27.4 wt% carbon and 70.0 wt% chlorine. Calculate the total chlorine consumption (kg/year) required to produce each grade of CPVC.

(b) Let X equal the fraction of the 300-day year in which 67% Cl CPVC is produced and (1 – x) the fraction in which 70% Cl CPVC is produced. Derive an expression for the gross annual profit [P(X) = sales revenue - raw material - cost manufacturing cost], assuming that all CPVC produced can be sold. Then determine the optimal value of X (the value that maximizes P) and the corresponding percentage increase in P over the profit attained if only 67% Cl CPVC is produced.

There is another complication. If the plant produces the new material for more than 30% of the year, there will be insufficient 67% Cl polymer to sell to existing customers. Marketing could put all customers on reduced allocation (so that all customers get a fixed percentage of the quantity they have received in the past), but the company could risk losing the business of its biggest customers. Alternatively, the company could continue to supply its biggest customers and stop selling the 67% material to some small customers. Unfortunately, most of the small customers have optimized their processes to use this polymer, and the cost of adapting their processes to a different polymer may be high enough to drive them out of business. Discuss these and other options available to the company, make a recommendation, and explain your reasoning.

Transcribed Image Text:

C67 ($/kg 67% Cl CPVC) 1.80 – (6.0 X 10-8)M67 !! C70 ($/kg 70% Cl CPVC) = 1.85 – (5.0 X 10-8)M70 + (4.0 × 10-14)(M70)?