Values of K 13.3 and K 13.5 can deviate significantly from unity; typical values for K 13.3

Values of K_ϕ13.3 and K_ϕ13.5 can deviate significantly from unity; typical values for K_ϕ13.3 range from 0.7 to 0.9 at a pressure of 7.5 MPa and typical MSR temperatures from 200°C to 320°C, while values for K_ϕ13.5 range from 0.8 to 0.95. Estimates of K_ϕi may be obtained from an equation of state, but such calculations are beyond the scope of the present discussion. Furthermore, computational alternatives often require a choice between simplified and more realistic, but complex, models. An instance that illustrates this situation is estimation K_ϕ13.3 of and K_ϕ13.5 for use in determining reaction equilibrium constants.

a. What physical model is invoked if it is assumed that K_ϕ13.3 = K_ϕ13.5 = 1.0?

b. In the calculations of Problem 13.15, K_ϕ13.3 and K_ϕ13.5 were taken to be 1.0. Determine the significance of the ideal gas assumptions by reestimating the conversions of CO and H₂ first with

K_ϕ13.3 = 0.7 and K_ϕ13.5 = 1.0, then with K_ϕ13.3 = 1.0 and K_ϕ13.5 = 0.8, and finally with K_ϕ13.3 = 0.7 and K_ϕ13.5 = 0.8.

c. From the preceding parts of this problem, what would be your decision (and why?) regarding inclusion of methods to estimate K_ϕ13.3 and K_ϕ13.5 in the process analysis?

Problem 13.15

As covered in the Process Description, there are three primary reactions that occur in the MSR. These are given by Equations 13.3, 13.4, and 13.5. However, determination of chemical equilibrium among the species H₂, CO, CO₂, H₂O, and CH₃OH involves only two of the three reactions because each reaction is a linear combination of the other two. Cherednichenko gives an approximation for the equilibrium relationships in Equation 13.3 (see Problem 13.13) and in Equation 13.5:

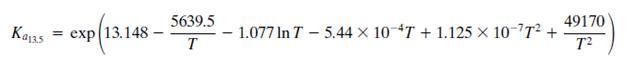
The equilibrium Ka_13.5 constant is defined by the relationship

Where T is in kelvin and K_ϕ13.5 accounts for nonideal behavior of the gas phase.

Transcribed Image Text:

5639.5 49170 Kaja5 exp(13.148 - 1.077 In T - 5.44 x 10-4T + 1.125 x 10-7T2 + T %3!