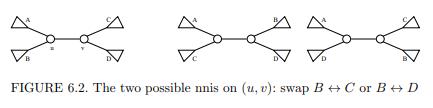
[40] In computational biology, evolutionary trees are represented by unrooted unordered binary trees with uniquely labeled leaves and unlabeled internal nodes. Measuring the distance between such trees is useful in biology. A nearest neighbor interchange (nni) operation swaps two subtrees that are separated by an internal edge (u, v), as shown in Figure 6.2.

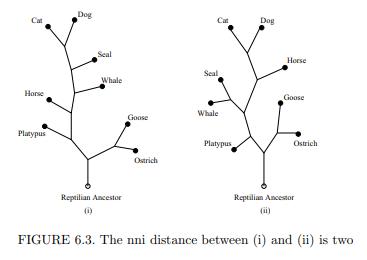
(a) Show that in Figure 6.3 it takes 2 nni moves to convert (i) to (ii).

(b) Show that n log n+O(n) nni moves are sufficient to transform a tree of n leaves to any other tree with the same set of leaves.

(c) Prove an Ω(n log n) lower bound for Item (b), using the incompressibility method.
Comments. Item

(b) is from [K. Culik II and D. Wood, Inform. Process.
Lett., 15(1982), 39–42; M. Li, J.T. Tromp, and L. Zhang, J. Theoret. Biology, 182(1996), 463–467]. The latter paper contains principal references related to the nni metric. Item

(c) is by D. Sleator, R.E. Tarjan, and W. Thurston [SIAM J. Discr. Math., 5(1992), 428–450], who proved the Ω(n log n) lower bound for a more general graph transformation system.

FIGURE 6.2. The two possible nnis on (u, v): swap B C or B D