[42] Consider a finite or countably infinite basis B, and define a probability function p : B → [0, 1] such that

b∈B p

(b) ≤ 1. If equality holds, we call the probability function proper. The squared Hellinger distance ρ(q, p) between two probability functions q and p is defined as

b∈B q

(b) − p(b)

2

. The χ2 distance, denoted by ρ2(q, p), is defined as

b∈B (q

(b) − p(b))2 /q(b). (Use 0/0 = 0 and ∞/∞ = 0.) If μ

is a semimeasure over B∗, and ω ∈ B∞, then the probability function

μ(·|ω1:n) : B → [0, 1] is defined by μ(b|ω1:n) = μ(ω1:nb)/μ(ω1:n). If μ is a measure and μ(ω1:n) = 0, then μ(·|ω1:n) is proper. The randomness deficiency of ω1:n with respect to μ is γ0(ω1:n|μ) = log(M(ω1:n)/μ(ω1:n)).

An infinite sequence ω is μ-random iff γ0(ω1:n|μ) = O(1).

(a) Suppose μ is a computable measure, σ is a computable semimeasure over B∗, and ω ∈ B∞. Show that

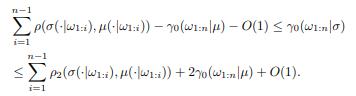
(b) Suppose that μ and σ are computable semimeasures over B∗, and ω ∈ B∞ is both μ-random and σ-random. Show that

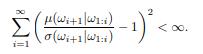
(c) Suppose μ is a computable measure, σ is a computable semimeasure over B∗, ω ∈ B∞ is σ-random, and μ(ω1:n) > 0 for all n. Show that ω is μ-random iff ∞
i=1 ρ(σ(·|ω1:i), μ(·|ω1:i))

(d) Show that if ω is both μ-random and σ-random, then μ(0|ω1:n) −
σ(0|ω1:n) → 0, as n → ∞.
Comments. Hint for Item (c): use Items

(a) and (b). Conclude from Item

(a) that if ω is random relative to a computable measure μ, and the computable measure σ is chosen so that γ0(ω1:n|σ) = o(n), then the mean squared Hellinger distance n−1 n−1 i=1 ρ(σ(·|ω1:i), μ(·|ω1:i)) goes to 0. Item

(c) gives a randomness criterion for objects with respect to a computable measure, in terms of Hellinger distance with a computable semimeasure with respect to which the object is known to be random.
Source: [V.G. Vovk, Soviet Math. Dokl., 35(1987), 656–660]. See also the estimate of prediction errors as in Theorem 5.2.1.

n-1 p((w), (W)) - Yo (w1:n ) - O(1) 10(1:10) i=1 VI n-1 P2 ( ( Wii) H (| W11)) + 270 (W1n|A) + O(1). i=1