Let where Xi i.i.d. 2 (1), i = 1, 2. (a) Describe Y in terms of a common density. (Hint: use Example 9.11). (b)

Let

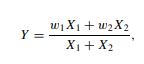
where Xi i.i.d. ∼ χ2 (1), i = 1, 2.

(a) Describe Y in terms of a ‘common’ density. (Hint: use Example 9.11).

(b) Assuming 0

(c) Show that it integrates to one. (Hint: substitute u = (y − w1) / (w2 − w1)).
Random variable Y is a special case of

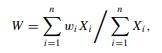
with n = 2. The density of W for n = 3 is more complicated, though still tractable, and is given in Provost and Cheong (2000). The distribution of W and of the more general random variable Y
AY/Y
BY, where Y ∼ Nn (µ, ) and A and B > 0 are n × n matrices, will be considered in a chapter on quadratic forms in Volume II.

Y = wX1+w2X2 X + X2