a. Beginning with the score function for the logit case in equation (11.5), show that the information matrix can be expressed as

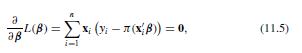\[\mathbf{I}(\boldsymbol{\beta})=\sum_{i=1}^{n} \sigma_{i}^{2} \mathbf{x}_{i} \mathbf{x}_{i}^{\prime}\]
where \(\sigma_{i}^{2}=\pi\left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}\right)\left(1-\pi\left(\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}\right)\right)\).

b. Beginning with the general score function in equation (11.4), determine the information matrix.

L-(8) = x; (y; -7(x,8)) = 0, (11.5) i-l