Consider a GB2 probability density function given in equation (17.3). a. Reparameterize the distribution by defining the
Question:
Consider a GB2 probability density function given in equation (17.3).
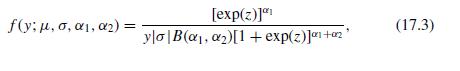
a. Reparameterize the distribution by defining the new parameter \(\theta=e^{\mu}\). Show that the density can be expressed as
\[\mathrm{f}_{G B 2}\left(y ; \theta, \sigma, \alpha_{1}, \alpha_{2}\right)=\frac{\Gamma\left(\alpha_{1}+\alpha_{2}\right)}{\Gamma\left(\alpha_{1}\right) \Gamma\left(\alpha_{2}\right)} \frac{(y / \theta)^{\alpha_{2} / \sigma}}{\sigma y\left[1+(y / \theta)^{1 / \sigma}\right]^{\alpha_{1}+\alpha_{2}}} .\]
b. Using part (a), show that a generalized gamma density.
\[\begin{aligned}\lim _{\alpha_{2} \rightarrow \infty} \mathrm{f}_{G B 2}\left(y ; \theta \alpha_{2}^{\sigma}, \sigma, \alpha_{1}, \alpha_{2}\right) & =\frac{1}{\sigma y \Gamma\left(\alpha_{1}\right)}(y / \theta)^{\alpha_{1} / \sigma} \exp \left(-(y / \theta)^{1 / \sigma}\right) \\& =\mathrm{f}_{G G}\left(y ; \theta, \sigma, \alpha_{1}\right)\end{aligned}\]
c. Using part (a), show that a Burr type 12 density.
\[\mathrm{f}_{G B 2}\left(y ; \theta, \sigma, 1, \alpha_{2}\right)=\frac{\alpha_{2}(y / \theta)^{\alpha_{2} / \sigma}}{\sigma y\left[1+(y / \theta)^{1 / \sigma}\right]^{1+\alpha_{2}}}=\mathrm{f}_{B u r r}\left(y ; \theta, \sigma, \alpha_{2}\right),\]
Step by Step Answer:

Regression Modeling With Actuarial And Financial Applications
ISBN: 9780521135962
1st Edition
Authors: Edward W. Frees





