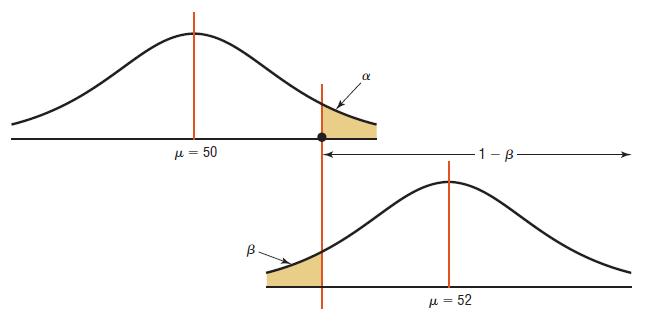
The power of a test (1 – b) can be calculated when a specific value of the mean is hypothesized in the alternative hypothesis; for example, let H₀ : µ = 50 and let H₁ : µ = 52. To find the power of a test, it is necessary to find the value of β. This can be done by the following steps:

Step 1    

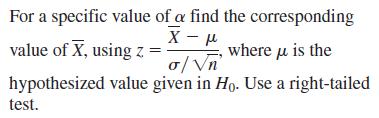
Step 2    

Using the value of X̅ found in step 1 and the value of µ in the alternative hypothesis, find the area corresponding to z in the

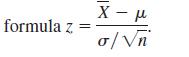Step 3 

Subtract this area from 0.5000. This is the value of β.

Step 4 

Subtract the value of β from 1. This will give you the power of a test. See Figure 8–41.

1. Find the power of a test, using the hypotheses given previously and α = 0.05, σ = 3, and n = 30.
2. Select several other values for µ in H₁ and compute the power of the test. Generalize the results.

Data from Figure 8-41

Transcribed Image Text:

For a specific value of a find the corresponding X-μ value of X, using z = where μ is the o/√n' hypothesized value given in Ho. Use a right-tailed test.