Excel and many other technologies are capable of generating normally distributed data drawn from a population with a specified mean and standard deviation. Bone density test scores are measured as z scores having a normal distribution with a mean of 0 and a standard deviation of 1. Generate two sets of sample data that represent simulated bone density scores, as shown below.

• Treatment Group: Generate 10 sample values from a normally distributed population of bone density scores with mean 0 and standard deviation 1.

• Placebo Group: Generate 15 sample values from a normally distributed population of bone density scores with mean 0 and standard deviation 1.

To generate sample data in Excel follow these steps (not available in Excel for Mac 2011):

1. Click the Data tab in the Ribbon.

2. Click the Data Analysis button in the Ribbon. (If Data Analysis is not available, the Data Analysis Toolpak must be installed as described in Section 1-4).

3. The Data Analysis dialog box now appears as shown on the next page.

4. Select Random Number Generation, and then click OK.

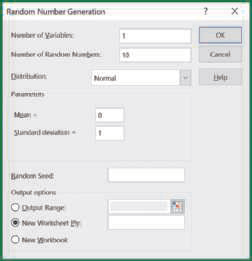
5. The Random Number Generation dialog box now appears.

a. Enter a value for the Number of Variables (or the number of columns of data), Number of Random Numbers, Mean, and Standard Deviation.

b. Select Normal in the Distribution box.

c. Click OK to generate the values.

Because each of the two samples consists of random selections from a normally distributed population with a mean of 0 and a standard deviation of 1, the data are generated so that both data sets really come from the same population, so there should be no difference between the two sample means.

a. After generating the two data sets, use a 0.10 significance level to test the claim that the two samples come from populations with the same mean.

b. If this experiment is repeated many times, what is the expected percentage of trials leading to the conclusion that the two population means are different? How does this relate to a type I error?

c. If your generated data leads to the conclusion that the two population means are different, would this conclusion be correct or incorrect in reality? How do you know?

d. If part (a) is repeated 20 times, what is the probability that none of the hypothesis tests leads to rejection of the null hypothesis?

e. Repeat part (a) 20 times. How often was the null hypothesis of equal means rejected? Is this the result you expected?