Compute the variance of (widehat{mu}) in (11.45) via the following steps. (a) Suppose the (N) subjects of
Question:
Compute the variance of \(\widehat{\mu}\) in (11.45) via the following steps.
(a) Suppose the \(N\) subjects of the population are labeled from 1 to \(N\). The \(i\) th subject with outcome \(y_{i}\) is sampled with the probability \(\pi_{i}\). Show that \(\widehat{\mu}=\frac{1}{N} \sum_{i=1}^{N} \frac{r_{i} y_{i}}{\pi_{i}}\), where \(r_{i}=1\) if the \(i\) th subject is sampled and 0 otherwise.
(b) Show that \(\operatorname{Cov}\left(\frac{r_{i} y_{i}}{\pi_{i}}, \frac{r_{j} y_{j}}{\pi_{j}}\right)= \begin{cases}\frac{y_{i}^{2}}{\pi^{2}} \pi_{i}\left(1-\pi_{i}\right) & \text { if } i=j, \\ \frac{\pi_{i j} y_{i} y_{j}}{\pi_{i} \pi_{j}} & \text { if } i eq j .\end{cases}\)
(c) Show that \(\operatorname{Var}(\widehat{\mu})=\frac{1}{N^{2}} \sum_{i, j}^{N}\left(\frac{\pi_{i j} y_{i} y_{j}}{\pi_{i} \pi_{j}}-y_{i} y_{j}\right)\).
(11.45)
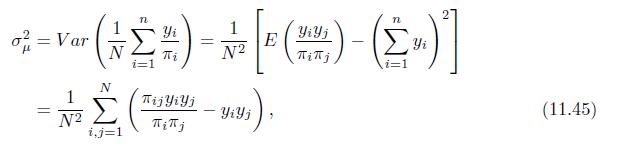
Step by Step Answer:

Applied Categorical And Count Data Analysis
ISBN: 9780367568276
2nd Edition
Authors: Wan Tang, Hua He, Xin M. Tu





