Consider the GLMM in (9.11), with a log link. Show that (a) (Eleft(y_{i t} mid mathbf{x}_{i t},
Question:
Consider the GLMM in (9.11), with a log link. Show that
(a) \(E\left(y_{i t} \mid \mathbf{x}_{i t}, \mathbf{z}_{i t}\right)=E\left[\left.\exp \left(\frac{1}{2} \mathbf{z}_{i t}^{\top} \Sigma_{b} \mathbf{z}_{i t}\right) \rightvert\, \mathbf{x}_{i t}\right] \exp \left(\mathbf{x}_{i t}^{\top} \boldsymbol{\beta}\right)\).
(b) if \(\mathbf{z}_{i t}\) is independent with \(\mathbf{x}_{i t}\), then \(E\left(y_{i t} \mid \mathbf{x}_{i t}\right)=\exp \left(\gamma_{0}+\mathbf{x}_{i t}^{\top} \boldsymbol{\beta}\right)\), where \(\gamma_{0}=\) \(\log \left[E\left(\exp \left(\frac{1}{2} \mathbf{z}_{i t}^{\top} \Sigma_{b} \mathbf{z}_{i t}\right)\right)\right]\).
(c) if \(\mathbf{z}_{i t}\) is a subvector of \(\mathbf{x}_{i t}\), say \(\mathbf{x}_{i t}=\left(\mathbf{z}_{i t}^{\top}, \mathbf{w}_{i t}^{\top}\right)^{\top}\), then
\[E\left(y_{i t} \mid \mathbf{x}_{i t}, \mathbf{z}_{i t}\right)=\exp \left[\mathbf{w}_{i t}^{\top} \boldsymbol{\beta}_{w}+\mathbf{z}_{i t}^{\top}\left(\boldsymbol{\beta}_{z}+\frac{1}{2} \Sigma_{b} \mathbf{z}_{i t}\right)\right]\]
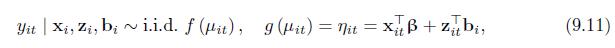
Step by Step Answer:

Applied Categorical And Count Data Analysis
ISBN: 9780367568276
2nd Edition
Authors: Wan Tang, Hua He, Xin M. Tu





