A large, hot plate hangs vertically in a room. Heat transfer from the plate to the air near it causes the air density to decrease. This lighter air rises upward with a velocity proportional to the group

\[ \left[\alpha_{T} g L\left(T_{p}-T_{f}\right)\right]^{1 / 2} \]

where \(\alpha_{T}\) is the coefficient of thermal expansion [units \(=\left({ }^{\circ} \mathrm{R}\right)^{-1}\) or \(\left.\mathrm{K}^{-1}\right], g\) is the acceleration of gravity, \(L\) is the plate length, and \(T_{p}\) and \(T_{f}\) are the temperatures of the plate and fluid, respectively, in \({ }^{\circ} \mathrm{R}\) or \(\mathrm{K}\). The resulting heat transfer process depends on the Grashof Number, defined by

\[ \mathrm{G}=\frac{ho^{2} \alpha_{T} g\left(T_{p}-T_{f}\right) L^{3}}{\mu^{2}} \]

where \(ho\) is density and \(\mu\) is dynamic viscosity. Show that \(\mathrm{G}\) is dimensionless. How is \(\mathrm{G}\) related to the common dimensionless parameters of fluid mechanics? Is it equivalent to a combination, power, or product of one or more of the common dimensionless parameters listed in Table 7.1?

Table 7.1

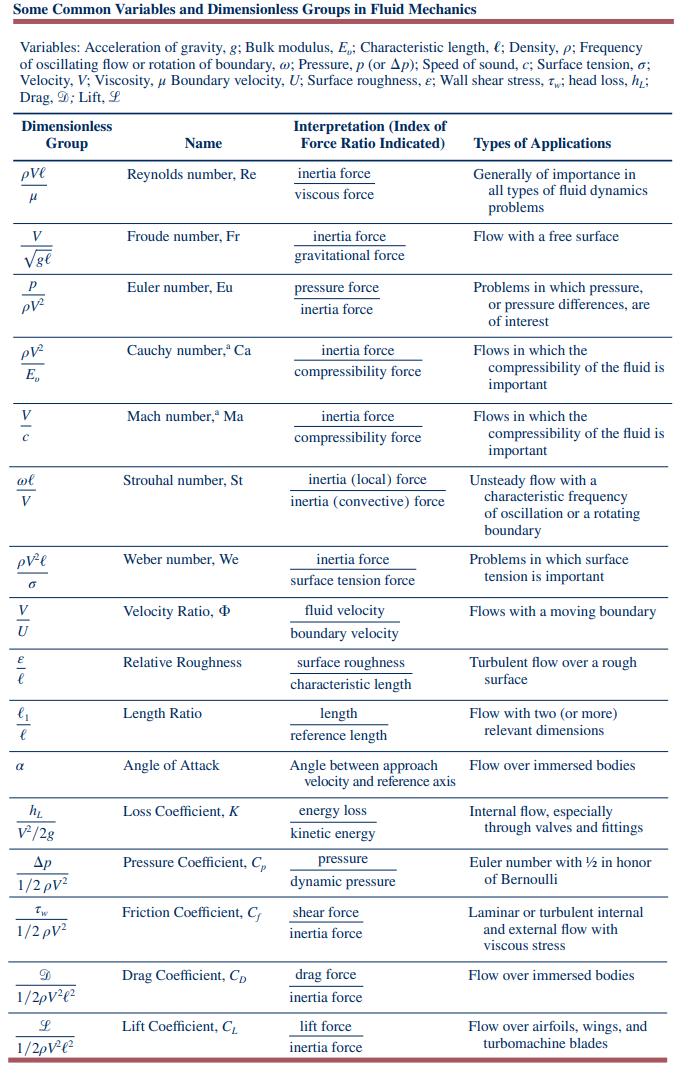
Transcribed Image Text:

Some Common Variables and Dimensionless Groups in Fluid Mechanics Variables: Acceleration of gravity, g; Bulk modulus, E.; Characteristic length, l; Density, p; Frequency of oscillating flow or rotation of boundary, o; Pressure, p (or Ap); Speed of sound, c; Surface tension, ; Velocity, V; Viscosity, Boundary velocity, U; Surface roughness, e; Wall shear stress, ; head loss, h; Drag, 9; Lift, L Dimensionless Group Name Interpretation (Index of Force Ratio Indicated) pve Reynolds number, Re inertia force viscous force Froude number, Fr gl Euler number, Eu P PV V C E Cauchy number, Ca Mach number," Ma wl Strouhal number, St V V >> Weber number, We inertia force gravitational force pressure force inertia force inertia force compressibility force inertia force compressibility force inertia (local) force inertia (convective) force inertia force surface tension force Velocity Ratio, U fluid velocity boundary velocity Relative Roughness surface roughness Length Ratio e Angle of Attack Loss Coefficient, K characteristic length length reference length Angle between approach velocity and reference axis energy loss kinetic energy pressure dynamic pressure h V/2g Ap 1/2 pv Pressure Coefficient, Cp Tw Friction Coefficient, C, 1/2 pV2 shear force inertia force D Drag Coefficient, CD drag force 1/201 inertia force L 1/2pV Lift Coefficient, CL lift force inertia force Types of Applications Generally of importance in all types of fluid dynamics problems Flow with a free surface Problems in which pressure, or pressure differences, are of interest Flows in which the compressibility of the fluid is important Flows in which the compressibility of the fluid is important Unsteady flow with a characteristic frequency of oscillation or a rotating boundary Problems in which surface tension is important Flows with a moving boundary Turbulent flow over a rough surface Flow with two (or more) relevant dimensions Flow over immersed bodies Internal flow, especially through valves and fittings Euler number with 1/2 in honor of Bernoulli Laminar or turbulent internal and external flow with viscous stress Flow over immersed bodies Flow over airfoils, wings, and turbomachine blades