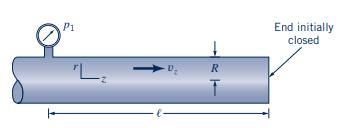
A liquid is contained in a pipe that is closed at one end as shown in Fig. P7.85. Initially the liquid is at rest, but if the end is suddenly opened the liquid starts to move. Assume the pressure \(p_{1}\) remains constant. The differential equation that describes the resulting motion of the liquid is

\[ ho \frac{\partial v_{z}}{\partial t}=\frac{p_{1}}{\ell}+\mu\left(\frac{\partial^{2} v_{z}}{\partial r^{2}}+\frac{1 \partial v_{z}}{r \partial r}\right) \]

where \(v_{z}\) is the velocity at any radial location, \(r\), and \(t\) is time. Rewrite this equation in dimensionless form using the liquid density, \(ho\), the viscosity, \(\mu\), and the pipe radius, \(R\), as reference parameters.

Figure P7.85

Transcribed Image Text:

P1 'L R T End initially closed