Consider the two-dimensional channel flow of Problem 6.3. Show that the given velocities satisfy conservation of mass in both differential and control volume forms.

Problem 6.3

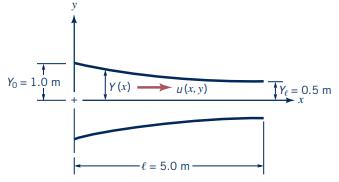
The flow in the plane two-dimensional channel shown in Figure P6.3 has \(x\) - and \(y\)-components of velocity given by

\[ \begin{aligned} & u=u_{0}\left(1+\frac{x}{\ell}\right)\left[1-\left(\frac{y}{Y}\right)^{2}\right] \\ & v=u_{0}\left[\frac{y^{3}}{\ell Y_{0}^{2}}\left(1+\frac{x}{\ell}\right)^{2}-\frac{y}{\ell}\right] \end{aligned} \]

Calculate the linear acceleration, rotation, vorticity, rate of volumentric strain, and rate of shear deformation for the flow.

Figure P6.3

Transcribed Image Text:

Yo= 1.0 m Y(x) u(x, y) - TY=0.5 m = 5.0 m