Determine the \(x\)-component of the acceleration, \(a_{x}\), along the centerline \((y=0)\) for the flow of Problem 4.20. Can you determine the acceleration vector at a location not on the centerline? Why or why not?

Problem 4.20

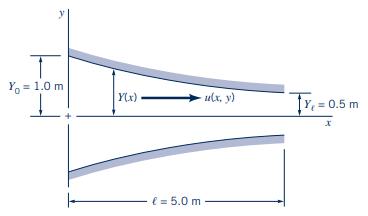
A constant-density fluid flows in the converging, twodimensional channel shown in Fig. P4.20. The width perpendicular to the paper is quite large compared to the channel height. The velocity in the \(z\) direction is zero. The channel half-height, \(Y\), and the fluid \(x\) velocity, \(u\), are given by

\[ Y=\frac{Y_{0}}{1+x / \ell} \quad \text { and } \quad u=u_{0}\left(1+\frac{x}{\ell}\right)\left[1-\left(\frac{y}{Y}\right)^{2}\right] \]

Where \(x, y, Y\), and \(\ell\) are in meters, \(u\) is in \(\mathrm{m} / \mathrm{s}, u_{0}=1.0 \mathrm{~m} / \mathrm{s}\), and \(Y_{0}=1.0 \mathrm{~m}\).

(a) Is this flow steady or unsteady? Is it one-dimensional, two-dimensional, or three-dimensional?

(b) Plot the velocity distribution \(u(y)\) at \(x / \ell=0,0.5\), and 1.0. Use \(y / Y\) values of 0 , \(\pm 0.2, \pm 0.4, \pm 0.6, \pm 0.8\), and \(\pm 1.0\).

Figure P4.20

Transcribed Image Text:

Y = 1.0 m Y(x) ulx, y) TY, = 0.5 m l=5.0 m