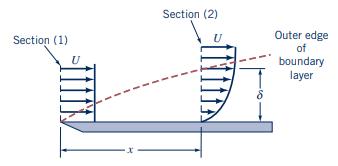
Flow of a viscous fluid over a flat plate surface results in the development of a region of reduced velocity adjacent to the wetted surface as depicted in Fig. P5.25. This region of reduced flow is called a boundary layer. At the leading edge of the plate, the velocity profile may be considered uniformly distributed with a value \(U\). All along the outer edge of the boundary layer, the fluid velocity component parallel to the plate surface is also \(U\). If the \(x\)-direction velocity profile at section (2) is

\[ \frac{u}{U}=\frac{3}{2}\left(\frac{y}{\delta}\right)-\frac{1}{2}\left(\frac{y}{\delta}\right)^{3} \]

develop an expression for the volume flowrate through the edge of the boundary layer from the leading edge to a location downstream at \(x\) where the boundary layer thickness is \(\delta\).

Figure P5.25

Transcribed Image Text:

Section (1) U Section (2) U Outer edge of boundary layer