The 20 ft wide rectangular channel shown has three different reaches. S₀,¹ = 0.01; S₀,² = 0.0004; S₀,  = 0.00317; Q = 500 cfs; n₁ = 0.015; normal depth for reach 2 is 5.4 ft and that for reach 3 is 2.7 ft. Determine the critical depth and normal depth for reach 1 (use Manning’s equation from §15.3). Then classify the flow in each reach (supercritical, subcritical, critical), and determine whether a hydraulic jump could occur. In which reach(es) might it occur if it does occur?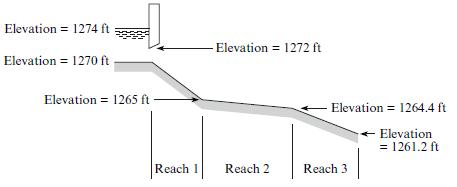

Elevation = 1274 ft - Elevation = 1272 ft Elevation = 1270 ft Elevation = 1265 ft Elevation = 1264.4 ft e Elevation = 1261.2 ft Reach 1 Reach 2 Reach 3