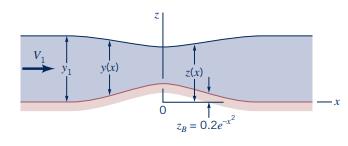
Water flows over the bump in the bottom of the rectangular channel shown in Fig. P10.16 with a flowrate per unit width of \(q=4 \mathrm{~m}^{2} / \mathrm{s}\). The channel bottom contour is given by \(z_{B}=0.2 e^{-x^{2}}\), where \(z_{B}\) and \(x\) are in meters. The water depth far upstream of the bump is \(y_{1}=2 \mathrm{~m}\). Plot a graph of the water depth, \(y=y(x)\), and the surface elevation, \(z=z(x)\), for \(-4 \mathrm{~m} \leq x \leq 4 \mathrm{~m}\). Assume onedimensional flow.

Figure P10.16

Transcribed Image Text:

y(x) 0 N z(x)