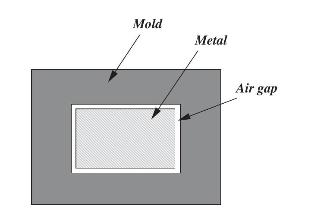
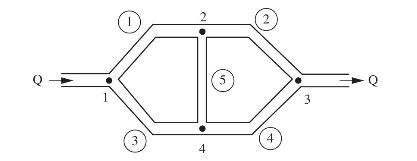
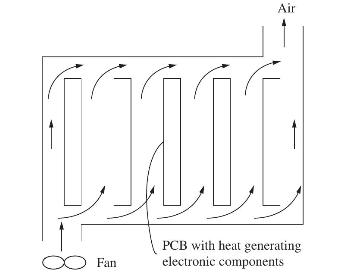
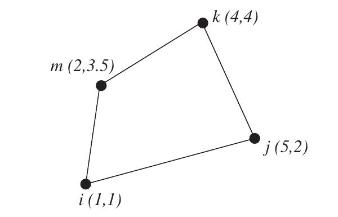
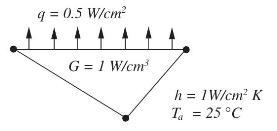
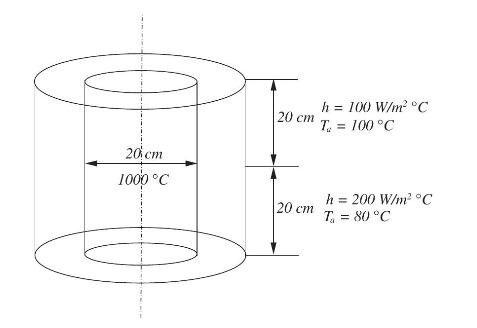
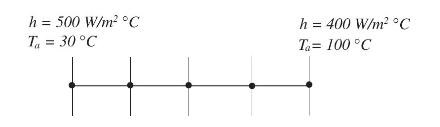
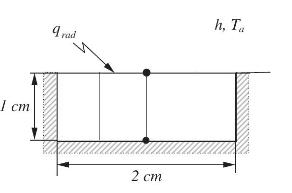
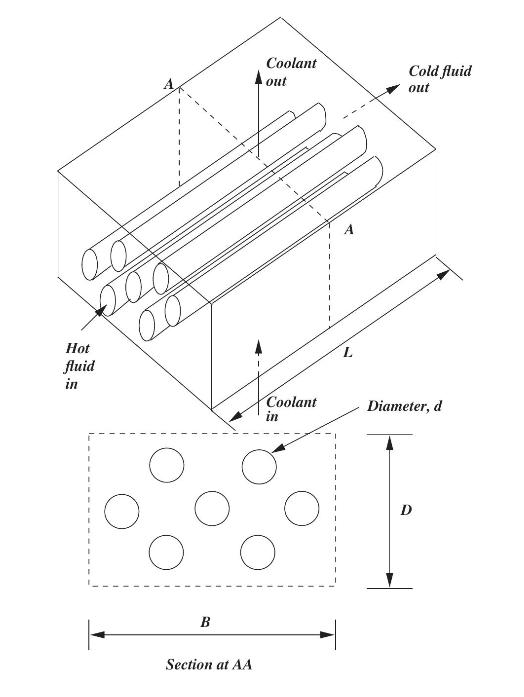
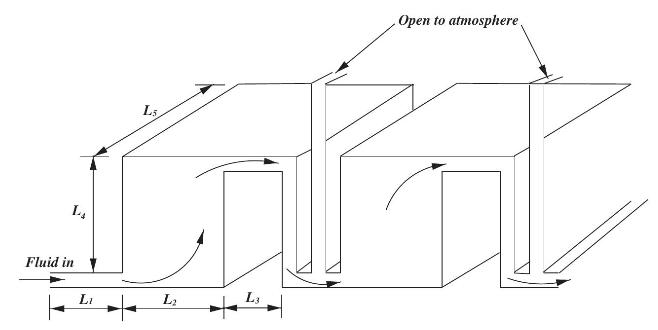
Fundamentals Of The Finite Element Method For Heat And Mass Transfer Wiley Series In Computational Mechanics 2nd Edition P. Nithiarasu, R. W. Lewis, K. N. Seetharamu - Solutions

Discover comprehensive support for "Fundamentals Of The Finite Element Method For Heat And Mass Transfer, 2nd Edition" with our expertly crafted solutions. Access the online answers key and delve into detailed solutions pdfs, featuring step-by-step answers and solved problems. Our solution manual and instructor manual provide thorough explanations to enhance your understanding. Explore chapter solutions and questions and answers to prepare effectively with the test bank. Enjoy the convenience of a free download for this essential textbook, ensuring you have all the resources needed to succeed.

In the above problem if the linear variation of temperature is replaced with a constant heat flux, determine the temperature and flow patterns.
Derive the energy balance equation for a rectangular fin of variable crosssection as shown in Figure 1.6. The fin is stationary and is attached to a hot heat source.
A closed plastic container used to serve coffee in a seminar room is made of two layers with an air gap placed between them. List all heat transfer processes associated with the cooling of the coffee in the inner plastic vessel. What steps do you consider for a better container design so as to
A square chip of size \(8 \mathrm{~mm}\) is mounted on a substrate with the top surface being exposed to a coolant flow at \(20^{\circ} \mathrm{C}\). All other surfaces of the chip are insulated. The chip temperature must not exceed \(80^{\circ} \mathrm{C}\) in order for the chip to function
Consider a person standing in a room, which is at a temperature of \(21^{\circ} \mathrm{C}\). Determine the total heat rate from this person if the exposed surface area of the person is \(1.6 \mathrm{~m}^{2}\) and the average outer surface temperature of the person is \(30^{\circ} \mathrm{C}\). The
A thin metal plate has one large insulated bottom surface and the top large surface exposed to solar radiation at a rate of \(600 \mathrm{~W} / \mathrm{m}^{2}\). The surrounding air temperature is \(20^{\circ} \mathrm{C}\). Determine the equilibrium surface temperature of the plate if the
A long, thin copper wire of radius \(r\) and length \(L\) has an electrical resistance of \(ho\) per unit length. The wire is initially kept at a room temperature of \(T_{a}\) and subjected to an electric current flow of I. The heat generation due to the current flow is simultaneously lost to the
In a continuous casting machine, the billet moves at a rate of \(\mathrm{m} / \mathrm{s}\). The hot billet is exposed to an ambient temperature of \(T_{a}\). Set up an equation to find the temperature of the billet as a function of time in terms of pertinent parameters. Assume that radiation also
In a double pipe heat exchanger, hot fluid (mass flow \(M \mathrm{~kg} / \mathrm{s}\) and specific heat \(\mathrm{C} \mathrm{kJ} / \mathrm{kg}{ }^{\circ} \mathrm{C}\) ) flows inside a pipe and cold fluid (mass flow \(\mathrm{m} \mathrm{kg} / \mathrm{s}\) and specific heat \(\mathrm{c}\)
Use the system analysis procedure described in this chapter and construct the discrete system for heat conduction through the composite wall shown in Figure 2.7. Also, from the following data, calculate the temperature distribution in the composite wall.Areas: \(A_{1}=2.0 \mathrm{~m}^{2}, A_{2}=1.0
The cross-section of an insulated pipe carrying a hot fluid is shown in Figure 2.8. The inner and outer radii of the pipe are \(r_{1}\) and \(r_{2}\) respectively. The thickness of the insulating material is \(r_{3}-r_{2}\). Assume appropriate conditions and form the discrete system equations.
The pipe network used to circulate hot water in a domestic central heating arrangement is shown in Figure 2.9. The flow rate at the entrance is \(\mathrm{Qm}^{3} / \mathrm{s}\). Neglecting any loss of mass, construct a system of simultaneous equations to calculate the pressure distribution at
A schematic diagram of a counter flow heat exchanger is shown in Figure 2.10. The hot fluid enters the central, circular pipe from the left and exits at the right. The cooling fluid is circulated around the inner tube to cool the hot fluid. Using the principles of heat exchanger system discussed in
A transient analysis is very important in the casting industry. In Figure 2.11, a simplified casting arrangement is shown (without a runner or raiser). The molten metal is poured into the mold and the metal loses heat to the mold and solidifies. It is often possible to have a small air gap between
Consider a \(0.6 \mathrm{~m}\) high and \(2 \mathrm{~m}\) wide double-pane window consisting of two \(4 \mathrm{~mm}\) thick layers of glass \(\left(k=0.80 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}\right)\) separated by a \(8 \mathrm{~mm}\) wide stagnant air space \(\left(k=0.025 \mathrm{~W} /
A simplified model can be applied to describe the steady-state temperature distribution through the core region, muscle region and skin region of the human body. The core region temperature \(T_{c}\), is the mean operating temperature of the internal organs. The muscle temperature, \(T_{m}\) is the
A composite wall consists of layers of aluminum, copper and steel. The steel external surface is \(350^{\circ} \mathrm{C}\) and the external surface of the aluminum is exposed to an ambient of \(25^{\circ} \mathrm{C}\) with a heat transfer coefficient of \(5 \mathrm{~W} / \mathrm{m}^{2}{ }^{\circ}
An incompressible fluid flows through a pipe network of circular pipes as shown in Figure 2.12. If \(0.1 \mathrm{~m}^{3} / \mathrm{s}\) of fluid enters and leaves the piping network, using a 4-node 5-element model, calculate the nodal pressure and the volume flow in each pipe. If the nodes 1 and 3
Figure 2.13 shows a direct current circuit. The voltage at the output terminals are also shown in Figure 2.13. Calculate the voltage at each node and the current in each of the branches using the finite element method. www V = 50 V www 3 10 ww 4 V = 30 V
A cross-section of a heat sink used in electronic cooling is shown in Figure 2.14. All the fins are of the same size. Calculate the heat dissipating capacity of the heat sink per unit length of heat sink. 8 mm 8 mm 100 C 2 mm 6 cm T. 25 C h = 100 W/mK k = 200 W/mK 8 mm. 8 mm
The details of a double pipe heat exchanger are given as: (a) cold fluid heat capacity rate \(C_{1}=1100 \mathrm{~W} /{ }^{\circ} \mathrm{C}\); (b) Hot fluid heat capacity rate \(C_{2}=734 \mathrm{~W} /{ }^{\circ} \mathrm{C}\); (c) overall heat transfer coefficient \(U=600 \mathrm{~W} /
Figure 2.15 shows an arrangement for cooling of an electronic equipment consisting of a number of printed circuit boards (PCB) enclosed in a box. Air is forced through the box by a fan. Select a typical element and write down the stiffness matrix and show that this method can take care of
A one-dimensional linear element is used to approximate the temperature variation in a fin. The solution gives the temperature at two nodes of an element as \(100^{\circ} \mathrm{C}\) and \(80^{\circ} \mathrm{C}\). The distances from the origin to node is \(6 \mathrm{~cm}\) and node \(j\) is \(10
A one-dimensional quadratic element is used to approximate the temperature distribution in a long fin. The solution gives the temperature at three nodes as 100, 90, and \(80^{\circ} \mathrm{C}\) at distances of \(10 \mathrm{~cm}, 15 \mathrm{~cm}\) and \(20 \mathrm{~cm}\) respectively from the
During the implementation of the finite element method, the evaluation of the integrals that contain shape functions and their derivatives is required. Evaluate the following integrals for a linear one-dimensional element\[ \begin{equation*} \int_{l} N_{i} d l ; \int_{l} N_{i}^{2} d l ; \int_{l}
Derive the shape functions for a one-dimensional linear element in which both the temperature and the heat fluxes should be continuously varying in the element. (Note that degrees of freedom for a one-dimensional linear element are \(T_{i}, q_{i}, T_{j}, q_{j}\).)
The solution for temperature distribution in a linear triangle gives the nodal temperature as \(T_{i}=200^{\circ} \mathrm{C}, T_{j}=180^{\circ} \mathrm{C}\) and \(T_{k}=160^{\circ} \mathrm{C}\). The coordinates of \(i, j\) and \(k\) are \(\left(x_{i}=2 \mathrm{~cm}, y_{i}=2
For a one-dimensional quadratic element evaluate the integrals. (Note: convert \(N_{i}, N_{j}\) and \(N_{k}\) to local coordinates and then integrate.)\[ \begin{equation*} \int_{l} N_{i} d l ; \int_{l} N_{j} d l ; \int_{l} N_{k} d l ; \int_{l} N_{i} N_{j} d l \tag{3.302} \end{equation*} \]
The nodal values for a rectangular element is given as follows, \(x_{i}=0.25 \mathrm{~cm}\), \(y_{i}=0.20 \mathrm{~cm}, x_{j}=0.30 \mathrm{~cm}, y_{m}=0.25 \mathrm{~cm}, T_{i}=150^{\circ} \mathrm{C}, T_{j}=120^{\circ} \mathrm{C}, T_{k}=100^{\circ} \mathrm{C}, T_{m}=110^{\circ} \mathrm{C}\)
Calculate the shape functions for a six-noded rectangle shown in Figure 3.31. 4 5 3 cm 2 3 cm 3 3 cm
Evaluate the partial derivatives of shape functions at \(\zeta=1 / 4\) and \(\eta=1 / 2\) of a quadrilateral element shown in Figure 3.32, assuming the temperature is approximated by (a) bilinear, (b) quadratic interpolating polynomials. m (2,3.5) k (4,4). i (1,1) j(5,2)
Calculate the derivatives \(\partial N_{6} / \partial x\) and \(\partial N_{6} / \partial y\) at a point \((2,5)\) for a quadratic triangle element shown in Figure 3.33 using local coordinates. (1,1) (2,7) (4,3)
In a double pipe heat exchanger, hot fluid flows inside a pipe and cold fluid flows outside in the annular space. The heat exchange between the two fluids is given by the differential equations, (refer to Exercise 2.5.12)Data From Exercise 2.5.12Exercise 2.5.12 The details of a double pipe heat
Calculate (using one, two and four elements) the temperature distribution and the heat dissipation capacity of a fin of length \(4 \mathrm{~cm}\) and cross-sectional dimensions of \(6 \mathrm{~mm} \times 4 \mathrm{~mm}\) with a heat transfer coefficient of \(0.1 \mathrm{~W} / \mathrm{m}^{2}{
A composite wall with three different layers, as shown in Figure 4.2 generates \(0.25 \mathrm{GW} / \mathrm{m}^{3}\) of heat. Using the relevant data given in Example 4.2.1, determine the temperature distribution across the wall using both linear and quadratic variations and compare the
An insulation system around a cylindrical pipe consists of two different layers. The first layer immediately on the outer surface of the pipe is made of glass wool and the second one is constructed using plaster of Paris. The pipe diameter is \(10 \mathrm{~cm}\) and each insulating layers is \(1
A solid cylinder of \(10 \mathrm{~cm}\) diameter generates \(0.3 \mathrm{GW} / \mathrm{m}^{3}\) of heat due to nuclear reaction. If the outside temperature is \(40^{\circ} \mathrm{C}\) and the heat transfer coefficient from the solid surface to the surrounding fluid is \(30 \mathrm{~W} /
A circular fin of inner diameter \(20 \mathrm{~cm}\) and outer diameter of \(26 \mathrm{~cm}\) transfers heat from a small motor cycle engine. If the average engine surface temperature is \(112^{\circ} \mathrm{C}\) determine the temperature distribution along the fin surface. The thermal
Consider a composite wall consisting of four different materials as shown in Figure 4.15. Assuming one-dimensional heat flow, determine the heat flow through the composite slab and the interfacial temperatures. \(k_{A}=200 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}, k_{b}=20 \mathrm{~W} /
Consider a composite wall, which has one linearly varying cross-sectional area as shown in Figure 4.16. Determine the heat flow and interfacial temperatures. Thickness \(=10 \mathrm{~cm}, k_{A}=200 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}, k_{B}=20 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}\)
A plane wall \(\left(k=20 \mathrm{~W} / \mathrm{m}{ }^{\circ} \mathrm{C}\right)\) of thickness \(40 \mathrm{~cm}\) has its outer surfaces maintained at \(30^{\circ} \mathrm{C}\). If there is uniform internal heat generation of \(0.2 \mathrm{MW} / \mathrm{m}^{3}\) in the plane wall, determine the
A plane wall \(\left(k=10 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}\right)\) of thickness \(50 \mathrm{~cm}\) has its exterior surface subjected to convection environment of \(30^{\circ} \mathrm{C}\) with a surface heat transfer coefficient of \(600 \mathrm{~W} / \mathrm{m}^{2}{ }^{\circ}
Calculate the outer wall surface temperature and the temperature distribution in a thick walled hollow cylinder when the inner wall temperature is \(120^{\circ} \mathrm{C}\) and the outer wall is exposed to a convection environment of \(25^{\circ} \mathrm{C}\) with a surface heat transfer
Calculate the surface temperature in a circular solid cylinder \((k=\) \(20 \mathrm{~W} / \mathrm{m}^{2} \mathrm{C}\) ) of radius \(30 \mathrm{~mm}\) with a volumetric heat generation of \(25 \mathrm{MW} / \mathrm{m}^{3}\). The external surface of the cylinder is exposed to a liquid at \(25^{\circ}
Consider a tapered fin of length \(5 \mathrm{~cm}\) dissipating heat to an ambient at \(30^{\circ} \mathrm{C}\). The heat transfer coefficient on the surface at the tip is \(100 \mathrm{~W} / \mathrm{m}^{2}{ }^{\circ} \mathrm{C}\). The fin tapers from a thickness of \(5 \mathrm{~mm}\) to a
A square plate size \(100 \mathrm{~cm} \times 100 \mathrm{~cm}\) is subjected to an isothermal boundary condition of \(500^{\circ} \mathrm{C}\) on the top and to convection environment (on all the remaining three sides) of \(100^{\circ} \mathrm{C}\) with a heat transfer coefficient of \(10
If in Exercise 5.8.1, there is a uniform heat generation of \(2{\mathrm{~W} / \mathrm{cm}^{3}}^{3}\) exists, and a line source of \(5 \mathrm{~W} / \mathrm{cm}\) at a location of \((x=30 \mathrm{~cm}\) and \(y=30 \mathrm{~cm})\), calculate the new temperature distribution using(a) Two triangles;(b)
Repeat Exercise 5.8.1 using(a) one rectangle;(b) four rectangles.Data From Exercise 5.8.1 A square plate size \(100 \mathrm{~cm} \times 100 \mathrm{~cm}\) is subjected to an isothermal boundary condition of \(500^{\circ} \mathrm{C}\) on the top and to convection environment (on all the remaining
Repeat Exercise 5.8. using(a) one rectangle;(b) four rectangles.Data From Exercise 5.8.1 A square plate size \(100 \mathrm{~cm} \times 100 \mathrm{~cm}\) is subjected to an isothermal boundary condition of \(500^{\circ} \mathrm{C}\) on the top and to convection environment (on all the remaining
In Exercise 5.8.1, if the thickness increases uniformly from \(1 \mathrm{~cm}\) from the bottom edge to \(3 \mathrm{~cm}\) at the top edge, rework the problem with(a) two triangles;(b) eight triangles.Data From Exercise 5.8.1 A square plate size \(100 \mathrm{~cm} \times 100 \mathrm{~cm}\) is
Calculate the stiffness matrix and loading vector for the axisymmetric element shown in Figure 5.19 with heat generation of \(G=1 \mathrm{~W} / \mathrm{cm}^{3}\), the heat transfer coefficient on the side ij is \(1.0 \mathrm{~W} / \mathrm{cm}^{2} \mathrm{~K}\) and the ambient temperature is
An Internal Combustion (IC) engine cylinder is exposed to hot gases at \(1000^{\circ} \mathrm{C}\) on the inside wall with a heat transfer coefficient of \(25 \mathrm{~W} / \mathrm{m}^{2} \mathrm{C}\) as shown in Figure 5.20. 20 cm 1000 C 20 cm h = 100 W/m C T = 100C h = 200 W/m C 20 cm T = 80C
A large block of steel with a thermal conductivity of \(40 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}\) and a thermal diffusivity of \(1.5 \times 10^{-5} \mathrm{~m}^{2} / \mathrm{s}\) is initially at a uniform temperature of \(25^{\circ} \mathrm{C}\). The surface is exposed to(a) A heat flux of
A fin of length \(1 \mathrm{~cm}\) is initially at the ambient temperature of \(30^{\circ} \mathrm{C}\). If the base temperature is suddenly raised to a temperature of \(150{ }^{\circ} \mathrm{C}\) and maintained at that value, determine the temperature distribution in the fin after 30 seconds if
A short aluminum cylinder \(2.5 \mathrm{~cm}\) in diameter and \(5 \mathrm{~cm}\) long is initially at a uniform temperature of \(100^{\circ} \mathrm{C}\). It is suddenly subjected to a convection environment at \(50{ }^{\circ} \mathrm{C}\) and \(h=400 \mathrm{~W} / \mathrm{m}^{2 \circ}
A plane wall of thickness \(4 \mathrm{~mm}\) has internal heat generation of \(25 \mathrm{MW} / \mathrm{m}^{3}\) with thermal properties of \(k=20 \mathrm{~W} / \mathrm{m}^{\circ} \mathrm{C}, p=8000 \mathrm{~kg} / \mathrm{m}^{3}\) and specific heat \(C_{p}=500 \mathrm{~J} / \mathrm{kg}{ }^{\circ}
A stainless steel plate size \(2 \mathrm{~cm} \times 1 \mathrm{~cm}\) is surrounded by an insulating block as shown in Figure 6.14 and is initially at a uniform temperature of \(40^{\circ} \mathrm{C}\) with a convection environment at \(40^{\circ} \mathrm{C}\). The top side of the plate is suddenly
Using a differential control volume approach, derive a three-dimensional convection-diffusion equation for pollution transport in a river.
Following the derivation of the CG method for a convection-diffusion equation discussed in this chapter, derive the CG method for a convection-diffusion equation with a source term \(Q\).
Derive Navier-Stokes equations in cylindrical and spherical coordinates.
Reduce the incompressible Navier-Stokes equations to solve a onedimensional time-dependent convection heat transfer problem.
For natural convection problems, if \(\alpha\) is replaced by \(v\) in the nondimensional scaling, derive the new nondimensional form.
Calculate laminar flow and heat transfer from a hot cylinder at \(R e=40\) placed inside a rectangular channel (assume the size) using the CBSflow code. Assume buoyancy effect is negligible. Determine the influence of the distance between the cylinder and the channel walls, inlet and exit.
Write a program in any standard scientific language to calculate stream functions from a computed velocity field.
In this example, you are asked to make appropriate assumptions and model flow past the heat exchanger tubes as shown in Figure 7.54.A schematic diagram of a typical cross flow heat exchanger arrangement is shown in Figure 7.54. As seen, the hot working fluid from the industry is passed through
In this exercise, you are asked to simulate the liquid flow through a liquid processing plant as shown in Figure 7.55.In the liquid processing industry, liquid is passed through several tanks as shown in Figure 7.55. The diagram shows a simplified model of such a plant. With appropriate
A two-dimensional square enclosure (all solid walls) filled with air is subjected to a linearly varying temperature on one of its vertical walls (say \(T=\left(x_{2} / L\right) T_{\max }\), where \(L\) is the characteristic dimension) and a constant temperature on the other vertical wall, which is

Fundamentals Of The Finite Element Method For Heat And Mass Transfer Wiley Series In Computational Mechanics 2nd Edition P. Nithiarasu, R. W. Lewis, K. N. Seetharamu - Solutions

Step by Step Answers