Consider the PDE problem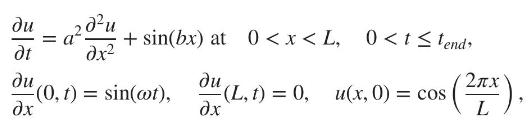

where \

(a, b\), and \(\omega\) are constants. Write the full finite difference discretization of the problem on a uniform grid. The discretization must be of the first order in time and second order in space. The answer should include the description of the grid and the finite difference schemes for the PDE and the boundary and initial conditions with specification of the grid points, at which each equation is applied.

dt = + sin(bx) at 0