For the specification in exercise 16.1, derive expressions for the elasticities of the probability of alternative j with respect to a change in X_ij and a change in X_ik, for k not equal to j.

The following exercises are based on data describing the choice of residential home heating systems in newly constructed homes in California. The dataset home_heating (available on the book’s website) was provided by Prof. Kenneth Train, and it forms the basis for homework assignments in his discrete choice econometrics course at UC-Berkeley. We observe 900 single-family homes that were newly built and have central air conditioning. Five types of home heating systems were considered feasible in these homes:

• central gas heating (j=1)
  room gas heating (j=2)
  central electrical heating (j=3)
  room electrical heating (j=4)
  heat pump (j=5).
• In addition to an indicator for choice, the dataset includes the following variables:
  id – unique identifier for each household ic₁, ic₂, ic₃, ic₄, ic₅ – installation cost (in 100s of USD) for each of the J=5 alternatives oc₁, oc₂, oc₃, oc₄, oc₅ – annual operating cost (in 100s of USD) for each of the J=5 alternatives income – annual income for the household (in 1,000s of USD) age – age of household head rooms – number of rooms in the house r₁, r₂, r₃, r₄ – dummy variables for the region of the state where the home is located.
• Regions include northern coast (r₁), southern coast (r₂), mountain region (r₃), and central valley (r₄). The installation and operating cost variables vary over both households and alternatives, while the income, age, region, and room count variables vary only over households.
• Data from exercise 16.1
• A useful feature of the conditional logit model with a specification including a full set of alternative specific constants is that
• 
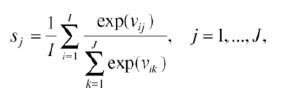
• where s_j is the proportion of times in the data that alternative j is selected, and the right-hand side is the average predicted probability for alternative j. Using the log-likelihood function in (16.13) and the specification v_ij=δ_j+βX_ij for j=1,..,J−1 and v_iJ=βX_iJ for j=J, show that the firstorder conditions with respect to δ₁,…,δ_J−1 for maximum likelihood estimation lead to (*) for all alternatives.

Transcribed Image Text:

exp(v;;) j=1,..., Lexp(v.) k=I