Suppose that firms can invest in abatement technology prior to permit trading. Firms have abatement cost functions C^j (e_j,κ_j), where κ_j is measured in money and lowers both the abatement and marginal abatement cost functions. More specifically:

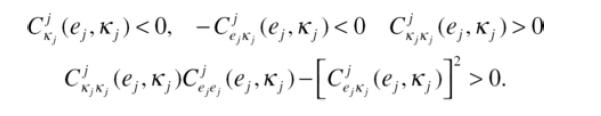
Consider three periods. In period 0 firms select the level of investment κ_j. In periods 1 and 2 firms choose abatement and engage in permit trading. The firm’s objective function is then given by: 

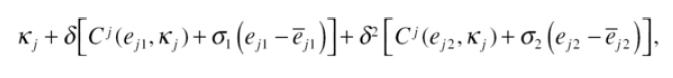
where δ is the discount factor and (e_j1 e _j2) and  are emissions and permit endowments, respectively, in periods 1 and 2.

(a) Characterize the firms’ cost minimization problem with respect to investment and emissions when no banking is allowed, and then when banking is allowed. Consider now the polluting sector’s aggregate abatement cost function C(E,K), which is assumed to have the same properties as the individual firms’ cost functions. Moreover assume the abatement cost functions are constant over time, and let L₁ and L₂ be the aggregate permit endowments.

(b) Determine the sector’s optimal investment level in the absence of banking. Investigate the comparative static effects of increasing L₁ and L₂ on the choice of K.

(c) Assume now that banking is allowed. Determine the amount of investment K and banking B.

(d) For the case of banking investigate the comparative static effects of increasing L₁ and L₂ on the choice of K and B.

(e) Assume now social damage is given by a convex social damage function D (E) that is constant over time. Determine the optimal levels of investment and pollution. Show that with competitive markets, the optimal level of investment will be chosen if the supply of permits corresponds to the optimal pollution level and banking is not allowed. What will happen if banking is allowed? Consider now an extension of the model with aggregate uncertainty. The sector’s abatement cost function is given by C(E,K,η), where η is a cost parameter that can take values η_L and η_H with probabilities pr and 1−pr, respectively. Assume also that the firms can increase their investment level in period 1 after observing η.

(f) Assume first that banking is not allowed and L₁ and L₂ are the aggregate permit endowments. Determine the optimal investment level K₀ in period 0. Determine the optimal investment level K₁ in period 1, as it depends on the observed cost parameter η.

(g) Assume now banking is allowed. Repeat the part (f) and compare the levels of investment. Investigate the comparative static effects of L₁ and L₂ on K₁ and B.

(h) For quadratic abatement costs C(E,K,η)=(η−E−K)²/2 and quadratic damage function D(E)=dE²/2 determine the optimal amount of permit quantities without banking, and the second-best optimal permit quantities when banking is allowed.

Transcribed Image Text:

C, (e, K;) <0, Cx, (e, K ) <0 C, (e, K ) > 0 C,K, (e, K) Ce, (e, K) - [Cx (e,,K)] > > 0.