We first assume thewind is uniform (w =constant,w1 = 0).Write the expression of the velocity of the boat along the axis of the wind vx = ˙x in terms of w and h(tan θ). For what values of θ and z′ is this velocity maximum? What is its value?

A sailboat has velocity v(θ), which is a function of the angle θ between the direction of the wind and the direction of the boat and also of the norm w of the velocity of the wind.We assume that the velocity of the boat v is proportional to the velocity of the wind w and that it depends on the angle θ chosen by the skipper. For convenience, in what follows, we shall write this velocity in the form

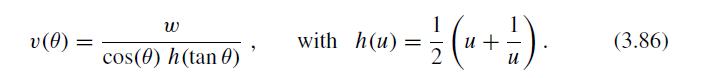
We are interested in the strategy where the sailboat tacks to the wind (i.e., θ ≤
π/2), as shown in Fig. 3.2. We assume that the x component vx of the velocity of the boat is opposite to that of the wind and that the position of the sailboat along the x axis always increases with time. We assume the coast is linear (land = half-plane z 0).
We assume the wind is parallel to the coast, of direction opposite to the x axis, and that the norm of its velocity w(z) depends only on the distance z to the coast.
Here, we assume that the velocity of the wind has the form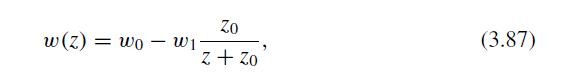

where w0 is the velocity far from the coast, which is larger than the velocity (w0 −
w1) ≥ 0 on the coast z = 0.

Transcribed Image Text:

N X=L Z = Z X W shore Fig. 3.2 Diagram of the direction of the sailboat v compared with that of the wind w 8