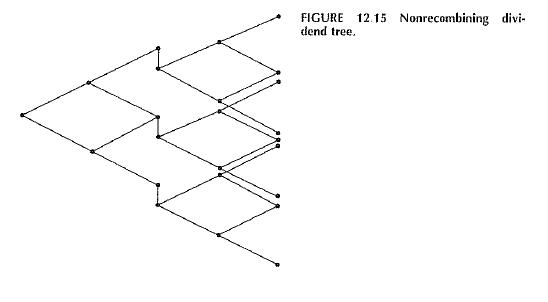
5. (Fixed dividende) Suppose that a stock will pay a dividend of amount D at time 7. We wish to determine the price of a European call option on this stock using the lattice method. Accordingly, the time interval [0, 7] covering the life of the option is divided into N intervals, and hence N + 1 time periods are assigned Assume that the dividend date r occurs somewhere between periods k and +1 One approach to the problem would be to establish a lattice of stock prices in the usual way, but subtract D from the nodes at period This produces a tree with nodes that do not recombine, as shown in Figure 12.15. The problem can be solved this way, but there is another representation that does recombine Since the dividend amount is known, we regard it as a nonrandom component of the stock price. At any time before the dividend we regard the price as having two components: a random component S and a deterministic component equal to the present value of the future dividend The random component S is described by a lattice with initial value 5(0) De" and with and d determined by the volatility of the stock. The option is evaluated on this lattice The only modification that must be made in the computation is that when valuing the option at a node, the stock price used in the valuation formula is not just S at that node, but rather SS + De-- for

Transcribed Image Text:

FIGURE 12.15 Nonrecombining divi- dend tree.