An investment bank has written 10,000 call options (strike 40, maturing in three months), and 5000 put
Question:
An investment bank has written 10,000 call options (strike 40, maturing in three months), and 5000 put options (strike 33, maturing in seven months), written on a stock share whose current price is \(S_{0}=36\). The risk-free rate is \(3 \%\), with continuous compounding, and the stock price volatility is \(36 \%\). How many stock shares should they hold in order to make the portfolio delta-neutral?
The value of the hedged portfolio depends on the prices of the two options and the underlying stock share:
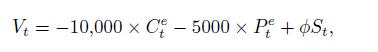
where the negative signs reflect the short positions in the two options, and is the number of stock shares, which may be positive or negative, depending on the yet unknown net exposure. The delta of the portfolio depends on the deltas of the two options:

We find the deltas of the two options by using Eqs. (13.28) and (13.29):![]() Hence, the delta of the hedged portfolio is
Hence, the delta of the hedged portfolio is
![]()
Note that the risk exposures from writing the two options tend to cancel each other, but the exposure due to the put options prevails. By setting \(=0\), we find
![]()
i.e., they should hold a short position in 125 stock shares.
Data From Equation (13.28)
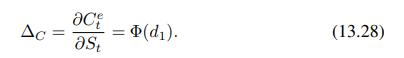
Data From Equation (13.29)
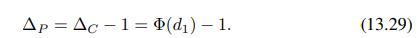
Step by Step Answer:

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte





