Consider the discrete-time stochastic process

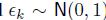where the initial state is often set to, and  is an element of a sequence of i.i.d. standard normals.  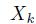is the state of the system at discrete time 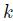, and it is a continuous random variable, since we add normal variables at each time step. Hence, we have a continuous-state, discrete-time stochastic process. The state is affected by a sequence of shocks 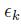, which are mutually independent, have zero expected value, and are also independent on the current state. Hence, the shocks are unpredictable. Note that we insist on adding a shock indexed byto a state variable indexed by 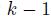, to emphasize the nature of the shocks, which are often referred to as innovations in econometric parlance. Their independence on the past is related to the efficient market hypothesis. This kind of process is called a random walk. As we shall see, there is a corresponding process in continuous time, called standard Wiener process, which plays a key role in financial modeling.By unfolding Eq. (11.1) recursively, we find 

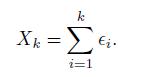
Given the mutual independence and the normality of the driving shocks, we easily find the unconditional distribution of the state,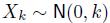. Please note that the variance is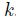. Hence, the standard deviation is 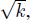i.e., it scales with the square root of (discrete) time. It is also easy to find conditional distributions. Conditional on the value 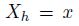at time  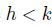we have

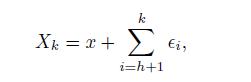
and

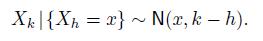
This is an example of a Gaussian process, since the joint distribution of the random variables 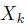is normal.

Data FromEq. (11.1) 

Transcribed Image Text:

XkXk-1+ k, k = 1,2,3,..., =