Consider the following stylized portfolio optimization problem:

- We represent uncertainty in asset return by a binomial model: There are two possible states of the world in the future, the up and down states, with probabilities, respectively.

- There are two assets: one is risk-free, the other one is risky.
- The risk-free asset has gain \(R_{f}\) in both states (recall that multiplicative gain is one plus holding period return; in other words, \(\$ 1\) grows to \(\$ R_{f}\) ).
- Current price for the risky asset is \(S_{0}\) and its gain is \(u\) in the up state and \(d\) in the down state. Hence, the two possible risky asset prices are \(u S_{0}\) and \(d S_{0}\). We use gain, rather than holding period return, to streamline notation.
- Initial wealth is \(W_{0}\) and the investor has logarithmic utility.
In this problem, there is actually one decision variable, which we may take as  , the number of stock shares purchased by the investor. To get rid of the budget constraint, we observe that \(S_{0}\) is the wealth invested in the risky asset, and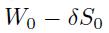 is invested in the risk-free asset. Then, future wealth will be, for each of the two possible states:

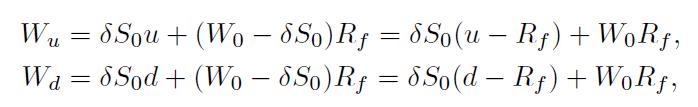
and expected utility is \(p \log \left(W_{u}\right)+q \log \left(W_{d}\right)\). The problem is then

 

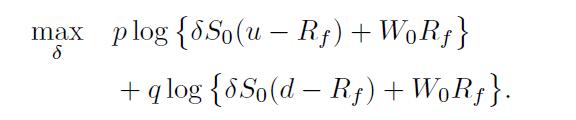
Let us write the first-order (stationarity) condition for optimality:

In order to solve for , we may rearrange the equation a bit:

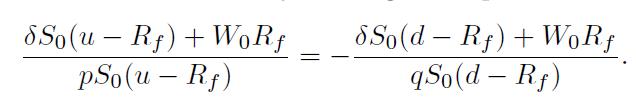
Straightforward manipulations yield

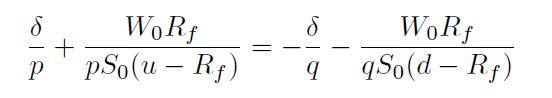
and

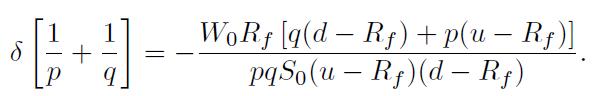
Then, one last step yields

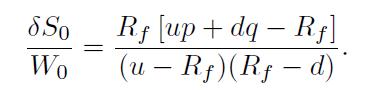
This relationship implies that the fraction of initial wealth invested in the risky asset does not depend on the initial wealth itself. We have derived this property in a simplified setting, but it holds more generally for logarithmic utility and is essentially due to its CRRA feature.

d- I = b