Let us assume that the following term structure prevails on markets:

A bond maturing in three years, paying a 3% annual coupon, has fair price

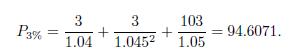
Note that the coupon rate is lower than all of the relevant rates, and the bond sells at discount. To find YTM, with annual compounding, we have to solve the nonlinear equation

which can be transformed into the polynomial equation

where  This equation has a single real root, as well as two complex conjugates that we ignore,

Note that the "average" is tilted toward the largest rate, corresponding to the last cash flow, which includes the face value and is much larger than those consisting of coupons only. A similar bond, with 9\% coupon, has fair price

This bond sells at premium, and its yield is 00495 . This is a bit smaller, as the first and second cash flows are relatively larger.

The difference in YTM may be quite significant. We omit the details, but if we consider similar bonds, paying one annual coupon with rates \(3 \%\) and \(9 \%\), respectively, maturing in 20 years, and we assume that the term structure consists of annually compounded rates, increasing linearly over time from \(2 \%\) to \(5 \%\), the two bond prices are

with yields

Transcribed Image Text:

T(0,1) =4%, r(0,2) = 4.5%, r(0,3) = 5%.