Let us consider a swap with the following features:

- Nominal amount, \(\$ 100,000\)

- Maturity, 14 months, so that cash flows will occur in 2, 8, and 14 months

- Swap rate, \(3.4 \%\) with semiannual compounding, so that the fixed payment is

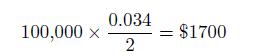
The current term structure, with continuous compounding, is

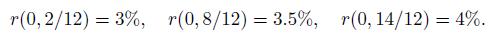
At the last reset time, four months ago, the six-month rate was \(3.8 \%\) with semiannual compounding, so that the next floating payment will be

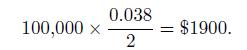
The value of the fixed-rate bond is

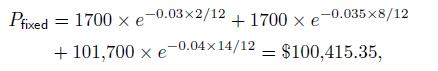
and its dollar duration is

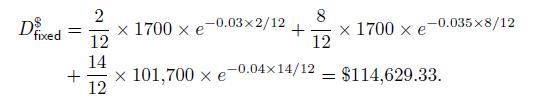
The value of the floating-rate bond is

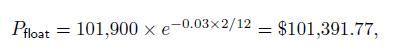
and its dollar duration is

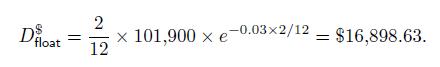
Hence, taking the viewpoint of the fixed payer, the value of the swap is 

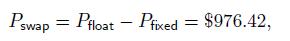
and its dollar duration is

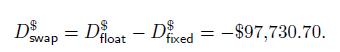
Let us consider an instantaneous parallel upshift of ten basis points in the term structure. According to the dollar duration approximation, the new swap value can be approximated by

 

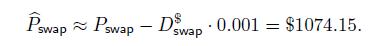
If we reprice the swap exactly, we find the following values after the shift:

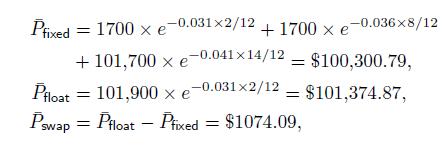
showing the accuracy of the approximation for a small shift.
We should note that, unlike plain bonds, the value of the swap may be increased by a rise in the the interest rates, which shows the potential of swaps for hedging interest rate risk. The increase in the swap value is slightly overestimated by the first-order approximation, whereas the loss on a bond is overestimated when using this kind of approximation. The explanation is provided by convexity vs. concavity (sometimes referred to as negative convexity) of the nonlinear functions that we are approximating to the first order.

Transcribed Image Text:

100,000 x 0.034 = $1700 2