Suppose that asset returns are uncorrelated, so that is a diagonal matrix, with entries . Then, the
Question:
Suppose that asset returns are uncorrelated, so that 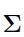 is a diagonal matrix, with entries
is a diagonal matrix, with entries 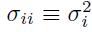 . Then, the weight for each risky asset \(i\) in the optimal portfolio, which also includes the risk-free asset, is
. Then, the weight for each risky asset \(i\) in the optimal portfolio, which also includes the risk-free asset, is
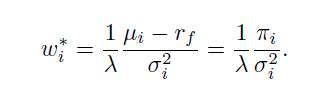
In this simplified case, portfolio weights depend in an obvious way on the risk aversion coefficient  , the risk premium
, the risk premium , and risk
, and risk  . We also observe that this solution is formally identical to the case of simple capital allocation; see Eq. (8.5).
. We also observe that this solution is formally identical to the case of simple capital allocation; see Eq. (8.5).
Data From Equation (8.5)

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte
Question Posted:





