The get a concrete feeling for the difficulties in integer programming, let us consider a pure integer LP borrowed from [35]:

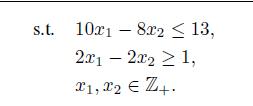
We might think that a simple way to get a good solution, even though not necessarily an optimal one, is to ignore the integrality constraints and solve the corresponding continuous LP. This need not yield an integer solution, but by judicious rounding we should be done. If we relax the integrality requirement, i.e., we just require 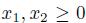, we find the optimal solution

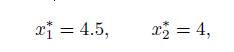
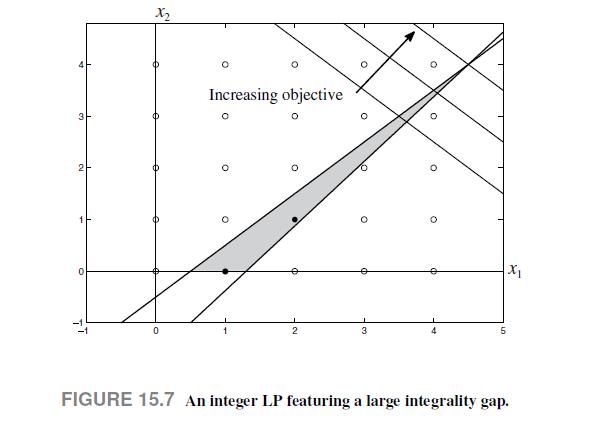
point, as one variable is already integer, and we may easily round the first one up or down to see what we get. Unfortunately, the solution (4; 4) is not feasible with respect to the second constraint, and the solution (5; 4) is not feasible with respect to the first one. Therefore, both trivially rounded solutions are not even feasible, and we are lost in our quest for optimality. In fact, the integer optimal solution is x1 = 2; x2 = 1, with optimal value 3. We get a clear picture from Fig. 15.7, where we plot the feasible integer set and the polyhedron corresponding to the continuous LP. The true feasible set consists of two points, and there is a large gap between the integer feasible set and the continuous LP polyhedron. This implies a significant gap between the objective function value of the optimal integer solution and the solution of the corresponding continuous LP.

Data From Fig. 15.7

Transcribed Image Text:

max 1+2