We are endowed with wealth \(W_{0}\) that we should allocate among a set of \(n\) assets with current price . At the end of a holding period of length \(T\), the prices of the assets are represented by continuous random variables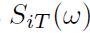. If we assume that assets are in-

finitely divisible and short-selling is not allowed, our decision can be represented by decision variables corresponding to the holding of each asset, i.e., the number of stock shares of firm \(i\) included in the portfolio.

Decision variables are subject to a budget constraint,

and define a random variable,

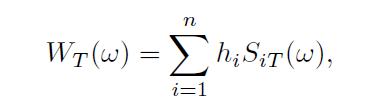
which is the random terminal wealth for each outcome In this case, the problem does not just require ranking a few simple lotteries. By choosing the portfolio holdings we define a continuous probability distribution of terminal wealth, and we might choose the most preferred one by defining and optimizing a suitable functional 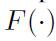, mapping a random variable into the set of real numbers:

We are talking about a functional rather than a function, since we are mapping random variables (which are function themselves, and not just numerical variables), to real numbers. If we can find a suitable functional 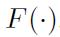, we may map a possibly complicated preference structure into the simple ordering of real numbers.

Transcribed Image Text:

Sio, i 1,...,n