We present an example where the representation of a bounded r.v. considered as the terminal variable of
Question:
We present an example where the representation of a bounded r.v. considered as the terminal variable of a martingale can be explicitly computed. et B be a Brownian motion and Ta=inf{t≥0:Bt=a} where a>0.
1. Using the Doléans-Dade exponential of λBλBλB, prove that, for λ>0λ>0λ>0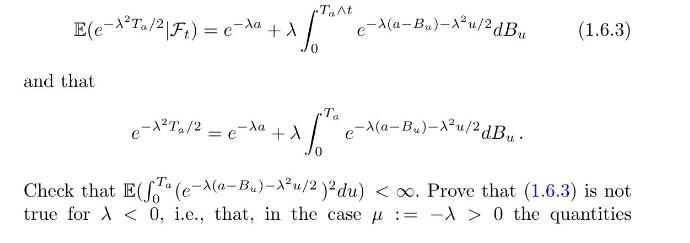

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Mathematical Methods For Financial Markets
ISBN: 9781447125242
1st Edition
Authors: Monique Jeanblanc, Marc Yor, Marc Chesney
Question Posted:





