(a) It is well known that the model in which air resistance is ignored, part (a)of Problem 36, predicts that the time t_ait takes the cannonball to attain its maximum height is the same as the time t_dit takes the cannonball to fall from the maximum height to the ground. Moreover, the magnitude of the impact velocity v_iwill be the same as the initial velocity v₀of the cannonball. Verify both of these results.

(b) Then, using the model in Problem 37 that takes air resistance into account, compare the value of t_a with t_d and thevalue of the magnitude of v_i with v₀. A root-fi­nding application of a CAS (or graphic calculator) may be useful here.

Data from problem 36

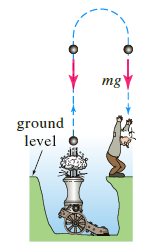
Suppose a small cannonball weighing 16 pounds is shot vertically upward, as shown in the following figure, with an initial velocity v₀ = 300 ft/s. The answer to the question €œHow high does the cannonball go?€ depends on whether we take air resistance into account.

Suppose air resistance is ignored. If the positive direction is upward, then a model for the state of the cannonball is given by d²s/dt² = -g (equation (12) of Section 1.3). Since ds/dt = v(t) the last differential equation is the same as dv/dt = -g, where we take g = 32 ft/s². Find the velocity v(t) of the cannonball at time t.

mg ground level