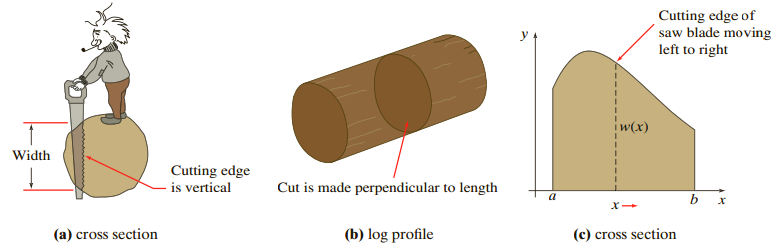
A long uniform piece of wood (cross sections are the same) is cut through perpendicular to its length by a vertical saw blade. See the figures . If the friction between the sides of the saw blade and the wood through which the blade passes is ignored, then it can be assumed that the rate at which the saw blade moves through the piece of wood is inversely proportional to the width of the wood in contact with its cutting edge. As the blade advances through the wood (moving, say, left to right) the width of a cross section changes as a nonnegative continuous function w. If a cross section of the wood is described as a region in the xy-plane de­fined over an interval [a, b] then, as shown in figure (c), the position x of the saw blade is a function of time t and the vertical cut made by the blade can be represented by a vertical line segment. The length of this vertical line is the width w(x) of the wood at that point. Thus the position x(t) of the saw blade and the rate dx/dt at which it moves to the right are related to w(x) by

w(x) dx/dt = k, x(0) = a.

Here k represents the number of square units of the material removed by the saw blade per unit time.

(a) Suppose the saw is computerized and can be programmed so that k = 1. Find an implicit solution of the foregoing initial-value problem when the piece of wood is a circular log. Assume a cross section is a circle of radius 2 centered at (0, 0).

(b) Solve the implicit solution obtained in part (b) for time t as a function of x. Graph the function t(x). With the aid of the graph, approximate the time that it takes the saw to cut through this piece of wood. Then fi­nd the exact value of this time.

Transcribed Image Text:

Cutting edge of ´saw blade moving left to right w(x) Width Cutting edge is vertical Cut is made perpendicular to length х (b) log profile (c) cross section (a) cross section