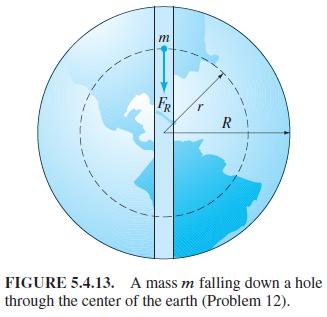
Assume that the earth is a solid sphere of uniform density, with mass M and radius R = 3960 (mi). For a particle of mass m within the earth at distance r from the center of the earth, the gravitational force attracting m toward the center is F_r = -GM_rm/r², where M_r is the mass of the part of the earth within a sphere of radius r (Fig. 5.4.13).

(a) Show that F_r = -GMmr/R³.

(b) Now suppose that a small hole is drilled straight through the center of the earth, thus connecting two antipodal points on its surface. Let a particle of mass m be dropped at time t = 0 into this hole with initial speed zero, and let r(t) be its distance from the center of the earth at time t , where we take r < 0 when the mass is “below” the center of the earth. Conclude from New-ton’s second law and part (a) that r'' (t) = -k²r(t), where k² = GM/R³ = g/R.

(c) Take g = 32.2 ft/s², and conclude from part (b) that the particle undergoes simple harmonic motion back and forth between the ends of the hole, with a period of about 84 min.

(d) Look up (or derive) the period of a satellite that just skims the surface of the earth; compare with the result in part (c). How do you explain the coincidence? Or is it a coincidence?

(e) With what speed (in miles per hour) does the particle pass through the center of the earth?

(f) Look up (or derive) the orbital velocity of a satellite that just skims the surface of the earth; compare with the result in part (e). How do you explain the coincidence? Or is it a coincidence?

Transcribed Image Text:

1 1 1 m FR\ r R FIGURE 5.4.13. A mass m falling down a hole through the center of the earth (Problem 12).