Consider the differential equation dx/dt = kx - x³. 

(a) If k ≦ 0, show that the only critical value c = 0 of x is stable.

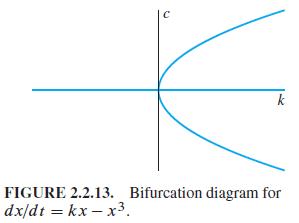
(b) If k > 0, show that the critical point c = 0 is now unstable, but that the critical points c = ±√k are stable. Thus the qualitative nature of the solutions changes at k = 0 as the parameter k increases, and so k = 0 is a bifurcation point for the differential equation with parameter k. The plot of all points of the form (k, c) where c is a critical point of the equation x' = kx - x³ is the "pitchfork diagram" shown in Fig. 2.2.13.

C k FIGURE 2.2.13. Bifurcation diagram for dx/dt = kx-x.