In (16) of Section 1.3 we saw that a mathematical model for the shape of a exible cable strung between two vertical supports is

dy/dx = W/T₁ €¦€¦€¦€¦€¦.. (11)

where W denotes the portion of the total vertical load between the points P₁ and P₂ shown in the following figure (1). The DE (11) is separable under the following conditions that describe a suspension bridge

Figure (1)

 

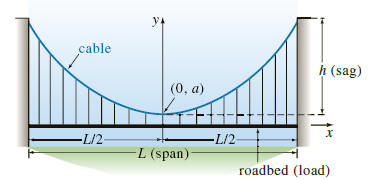
Let us assume that the x- and y-axes are as shown in the following figure (2) that is, the x-axis runs along the horizontal roadbed, and the y-axis passes through (0, a), which is the lowest point on one cable over the span of the bridge, coinciding with the interval [-Ly2, Ly2]. In the case of a suspension bridge, the usual assumption is that the vertical load in (11) is only a uniform roadbed distributed along the horizontal axis. In other words, it is assumed that the weight of all cables is negligible in comparison to the weight of the roadbed and that the weight per unit length of the roadbed (say, pounds per horizontal foot) is a constant . Use this information to set up and solve an appropriate initial-value problem from which the shape (a curve with equation y = φ(x)) of each of the two cables in a suspension bridge is determined. Express your solution of the IVP in terms of the sag h and span L. See the following figure (2).

(2)

Transcribed Image Text:

(a) suspension bridge cable (b) telephone wires Ун cable h (sag) (0, a) -L/2- L (span) -L/2- roadbed (load)