In Problem 19, what is a differential equation for the displacement x(t) if the motion takes place in a medium that imparts a damping force on the spring/ mass system that is proportional to the instantaneous velocity of the mass and acts in a direction opposite to that of motion?

Data from problem 19

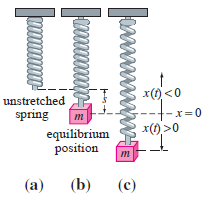
After a mass m is attached to a spring, it stretches it s units and then hangs at rest in the equilibrium position as shown in the following figure (b). After the spring/mass system has been set in motion, let x(t) denote the directed distance of the mass beyond the equilibrium position. As indicated in following figure (c), assume that the downward direction is positive, that the motion takes place in a vertical straight line through the center of gravity of the mass, and that the only forces acting on the system are the weight of the mass and the restoring force of the stretched spring. Use Hooke€™s law: The restoring force of a spring is proportional to its total elongation. Determine a differential equation for the displacement x(t) at time t > 0.

 

x() 0 equilibrium position (b) (a) (c) wwwwwwa