In Problems 36 and 37, a mass–spring–dashpot system with external force f (t) is described. Under the assumption that x(0) = x'(0) = 0, use the method of Example 7 to find the transient and steady periodic motions of the mass. Then construct the graph of the position function x(t). If you would like to check your graph using a numerical DE solver, it may be useful to note that the function

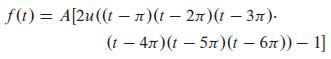
has the value + A if 0

m = 1, k = 10, c = 2; f(t) is a square wave function with amplitude 10 and period 2π.

f(t) = A[2u((t)(1-2)(t - 3). (t - 4)(t - 5)(t - 6)) - 1]