Problems 20 through 23 deal with the same system of three railway cars (same masses) and two buffer springs (same spring constants) as shown in Fig. 7.5.6 and discussed in Example 2. The cars engage at time t = 0 with x₁(0) = x₂ (0) = x₃ (0) = 0 and with the given initial velocities (where v₀ = 48 ft/s). Show that the railway cars remain engaged until t = π/2 (s), after which time they proceed in their respective ways with constant velocities. Determine the values of these constant final velocities x'₁ (t), x'₂ (t), and x'₃ (t) of the three cars for t > π/2. In each problem you should find (as in Example 2) that the first and third railway cars exchange behaviors in some appropriate sense.

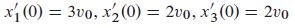
Transcribed Image Text:

Example 2 k₂ kz m₁ www.com m₂ www m3 ooooooo 00000000 00:00 0000 FIGURE 7.5.6. The three railway cars of Example 2. Railway cars Figure 7.5.6 shows three railway cars connected by buffer springs that react when compressed, but disengage instead of stretching. With n = 3, k2 = k3 = k, and k₁ k4= 0 in Eqs. (2) through (4), we get the system which is equivalent to with -k k [-]-[40] = k -2k m3 m1 m2 and X" = corresponding to the natural frequencies @₁ = 0, C₁ = -C1 C2 0 λ₁ = 0, λ2 = -c1, C₁ = Hence the coefficient matrix A is k mi If we assume further that m₁ = m3, so that c₁ = C3, then a brief computation gives -λ(a + c)(a + c₁ +20₂) = 0 (20) for the characteristic equation of the coefficient matrix A in Eq. (18). Hence the matrix A has eigenvalues C1 -202 C3 @2 = √√C₁, m₁ = m3 = 750, 3000 750 A = = 4, (i = 1, 2, 3). -4 6 0 0 C2 -C3 k -k C₂ = A3-C1-2c2 of the physical system. For a numerical example, suppose that the first and third railway cars weigh 12 tons each, that the middle car weighs 8 tons, and that the spring constant is k = 1.5 tons/ft; i.e., k = 3000 lb/ft. Then, using fps units with mass measured in slugs (a weight of 32 pounds has a mass of 1 slug), we have X W3 = √c1 +2c₂2 m₂ = 500. 4 0 -12 6 4 -4 k 3000 500 . X, = 6. (17) (18) (19) (21a) (21b) (22) and the eigenvalue-frequency pairs given by (21a) and (21b) are λ₁ = 0, ₁ = 0; λ₂ = -4, w2 = 2; and λ3 = -16, 03 = 4.