Question: Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0

Problems 24 through 34 deal with a mass–spring–dashpot system having position function x(t) satisfying Eq. (4). We write x0 = x(0) and v0 = x'(0) and recall that

p = c/(2m), w = k/m, and w=w2 - p.

The system is critically damped, overdamped, or underdamped, as specified in each problem.

(Underdamped) Let x1 and x2 be two consecutive local maximum values of x (t). Deduce from the result of Problem 32 that 

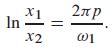
The constant Δ = 2πp/ω1 is called the logarithmic decrement of the oscillation. c = mω1Δ/π because p = c/(2m).

p = c/(2m), w = k/m, and w=w2 - p.

Step by Step Solution

★★★★★

3.54 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

If x x t and x x t are two succe... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Problems 24 through 34 deal with a massspringdashpot system having position function x(t) satisfying Eq. (4). We write x 0 = x(0) and v 0 = x'(0) and recall that The system is critically damped,...

Q:

Norman Kluz bid for and won a concession to rent bicycles in the local park during the summer. During June, he completed the following transactions for his business: June 2 Began business by placing...

Q:

Give the structure for each of the following. a. 3-hexene b. 2,4-heptadiene c. 2-methyl-3-octene d. 4-methyl-1 -pentyne

Q:

Oil wells. How much oil the wells in a given field will ultimately produce is key information in deciding whether to drill more wells. Here are the estimated total amounts of oil recovered from 64...

Q:

5. Decomposition of a time series involves breaking down the historical data into explained and unexplained variation. Mark the statement as T (True) or F (False).

Q:

Consider a manufacturing process that is producing hypodermic needles that will be used for blood donations. These needles need to have a diameter of 1.65 mmtoo big and they would hurt the donor...

Q:

Recall that the two errors discussed in this chapter were regarded as false alarm and missed opportunity. In some fields, these errors are also regarded as consumers risk and producers risk. With...

Q:

Suppose that you are considering whether to publish a weekly alternative newspaper on campus. You decide to survey a random sample of students on your campus to ask if they would be likely to read...

Q:

Check my work Exercise 20-34 Budgeted income statement LO P3 10 points Fortune, Inc., is preparing its master budget for the first quarter. The company sells a single product at a price of $25 per...

Q:

investments types under equity and debt and treatment methods ? [Provide explanation and type your answer and do not copy the answer from chegg study ] this is second time i am posting this...

Q:

Write a literature review of hospitality internship