Problems 43 through 46 concern the differential equation where k is a constant. Suppose a population P
Question:
Problems 43 through 46 concern the differential equation
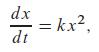
where k is a constant.
Suppose a population P of rodents satisfies the differential equation dP/dt = kP2. Initially, there are P(0) = 2 rodents, and their number is increasing at the rate of dP/dt = 1 rodent per month when there are P = 10 rodents. Based on the result of Problem 43, how long will it take for this population to grow to a hundred rodents? To a thousand? What’s happening here?
FIGURE 1.1.8. Graphs of solutions of the equation dy/dx = y2.
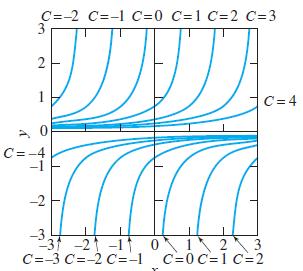
Problem 43
(a) If k is a constant, show that a general (one-parameter) solution of the differential equation is given by x(t) = 1/(C - k t), where C is an arbitrary constant.
(b) Determine by inspection a solution of the initial value problem x' = kx2, x(0) = 0.
Step by Step Answer:

Differential Equations And Linear Algebra
ISBN: 9780134497181
4th Edition
Authors: C. Edwards, David Penney, David Calvis





